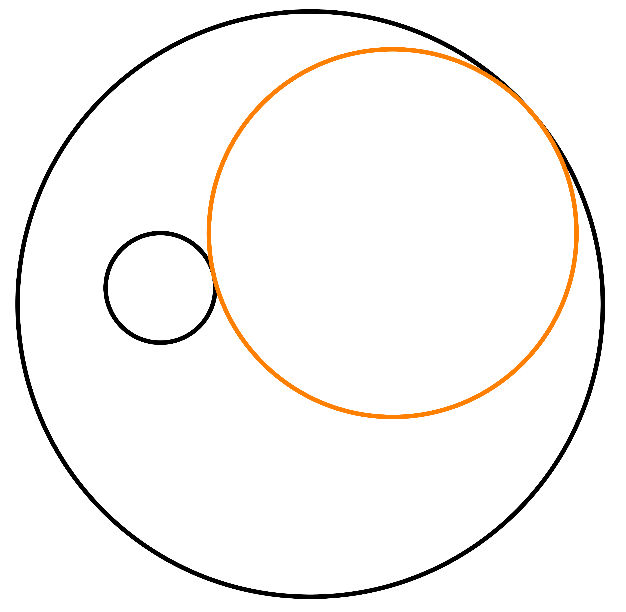
Wyobraźmy sobie dwa okręgi, jeden z nich zawarty wewnątrz koła drugiego – czarne okręgi na rysunku poniżej po lewej stronie. Nazwijmy je okręgami bazowymi. Wiadomo, że można skonstruować trzeci okrąg, styczny do obu tych okręgów – okrąg żółty.

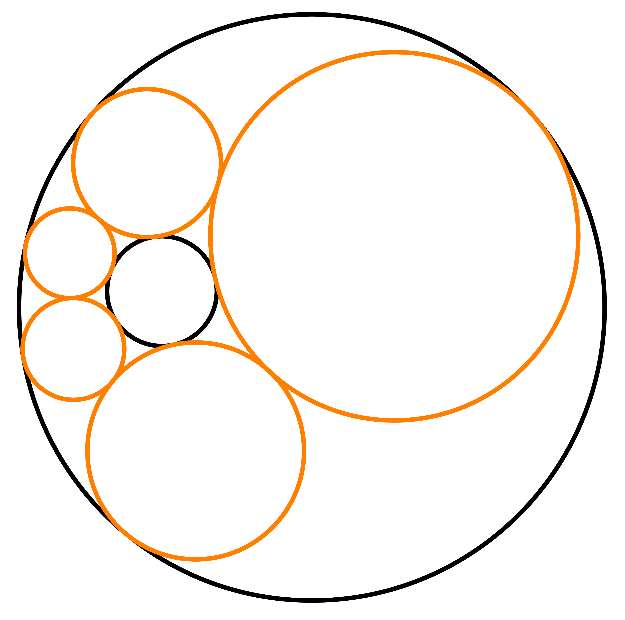
Ale czy da się skonstruować kolejne okręgi tak, by były styczne do okręgów bazowych i do wszystkich utworzonych wcześniej? Dla przykładu ciąg pięciu tak skonstruowanych okręgów ilustruje rysunek u góry po prawej stronie. Zbiór tak utworzonych okręgów nosi nazwę poryzmu Steinera.

Słowo poryzm opisał już Euklides w swoich trzech księgach, które niestety zaginęły. Oznacza ono, że jeśli potrafimy utworzyć jeden obiekt spełniający pewną własność, to możemy utworzyć jeszcze n obiektów spełniających tę własność, a jeśli nie potrafimy go utworzyć, to nie ma żadnego takiego obiektu.

We współczesnym użyciu poryzm jest relacją, która utrzymuje się dla nieskończonego zakresu wartości, ale tylko przy założeniu pewnego warunku. W naszym przypadku warunkiem, który musi być spełniony jest styczność każdego z n okręgów do dwóch sąsiednich i do dwóch ustalonych bazowych okręgów.

Gdybyśmy skonstruowali n takich okręgów (gdzie n jest liczbą naturalną), przy czym n-ty okrąg byłby styczny do pierwszego, to zamknęlibyśmy ciąg tych n okręgów w pewnym łańcuchu zwanym łańcuchem okręgów Steinera. Ponieważ łańcuch ten spełnia własność poryzmu stąd jego nazwa Poryzm Steinera.

Poniżej zamieszczony jest aplet GeoGebry takiego poryzmu zamykający łąńcuch pięciu okręgów. Jak skonstruować taki aplet, opisałem w artykule nr 64/2021 w czasopiśmie „Świat Matematyki”.