Poryzm Steinera
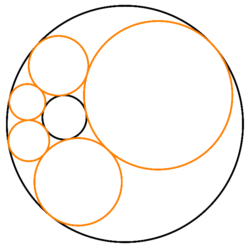
Wyobraźmy sobie dwa okręgi, jeden z nich zawarty wewnątrz koła drugiego – czarne okręgi na rysunku poniżej po lewej stronie. Nazwijmy je okręgami bazowymi. Wiadomo, że można skonstruować trzeci okrąg, styczny do obu tych okręgów – okrąg żółty. Ale czy da się skonstruować kolejne okręgi tak, by były styczne do okręgów bazowych i do wszystkich Read more about Poryzm Steinera[…]