Sześcian to najbardziej popularny wielościan występujący w programie szkolnym matematyki. Wiemy o nim wiele, ale czy tak naprawdę znamy wszystkie problemy związane z sześcianem? Spróbujmy zgłębić takie zagadnienia jak przekroje sześcianu, specjalne ułożenie sześcianu zwane sześcianem diagonalnym oraz kilka zadań które wydają się łatwe, a jednak możemy popełnić w nich istotny błąd.
Przekroje sześcianu (cross-sections of the cube)
Temat ten przewija sie wielokrotnie na lekcjach w szkole podstawowej, w liceum i na egzaminach. Poniżej są zilustrowane najbardziej typowe przekroje które warto znać, a na kanwie których konstruowane są czasami zadania.
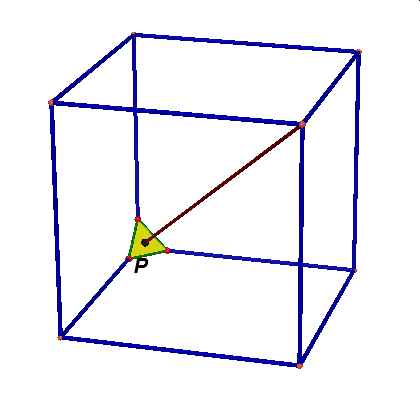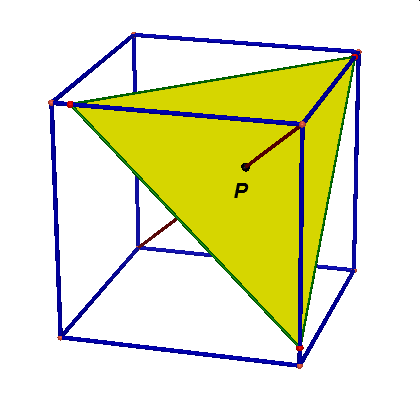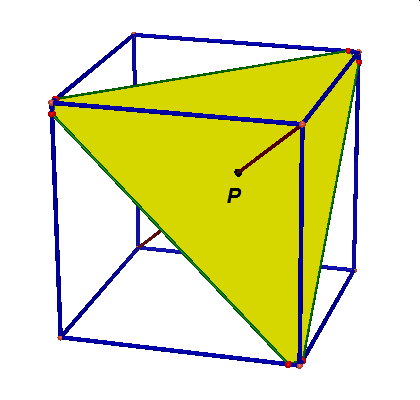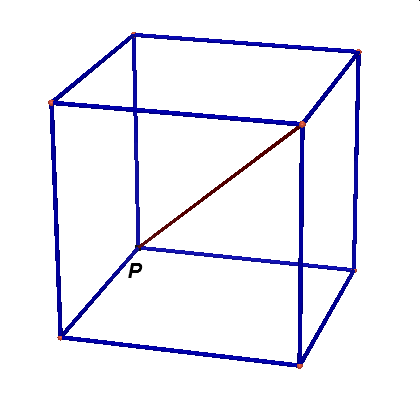

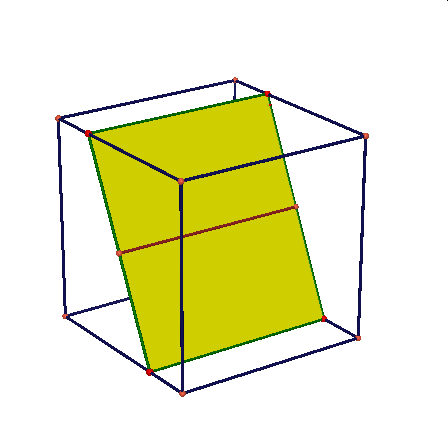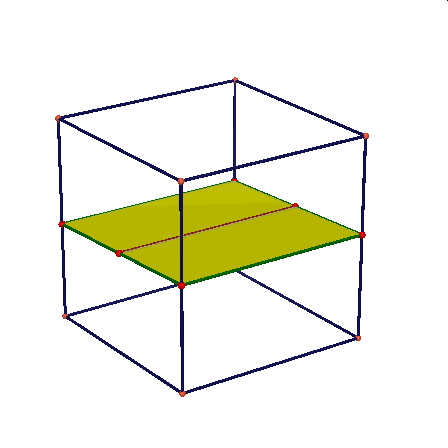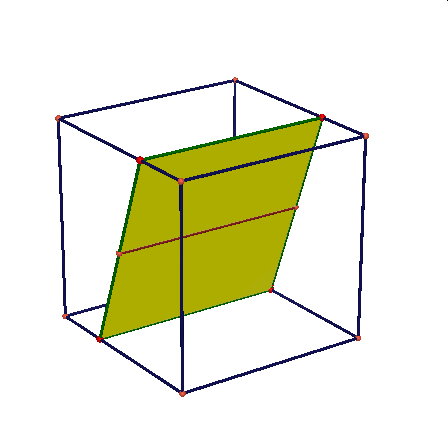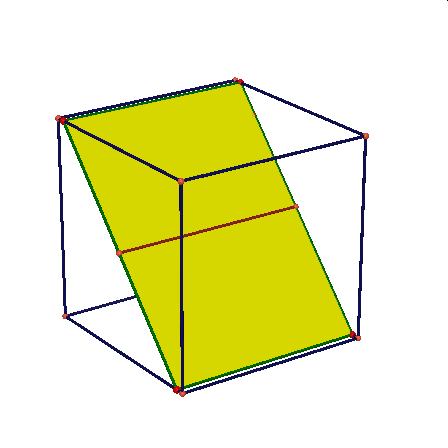
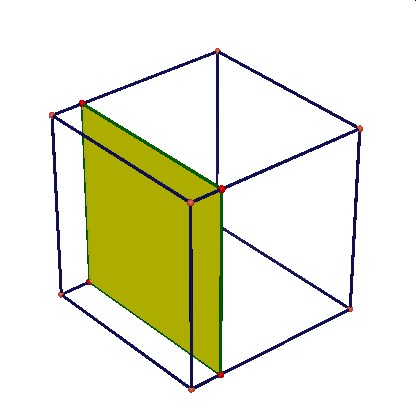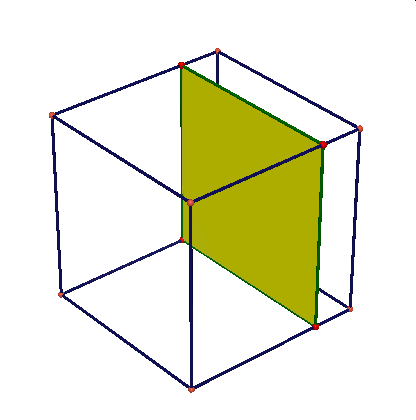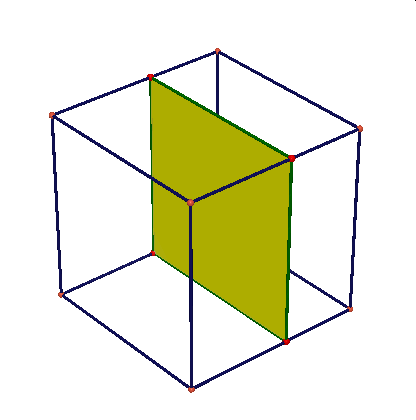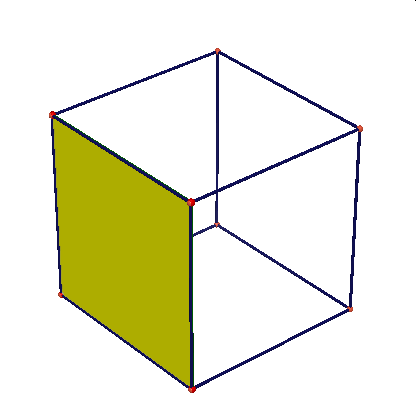

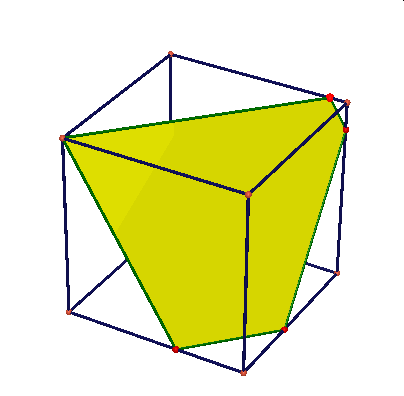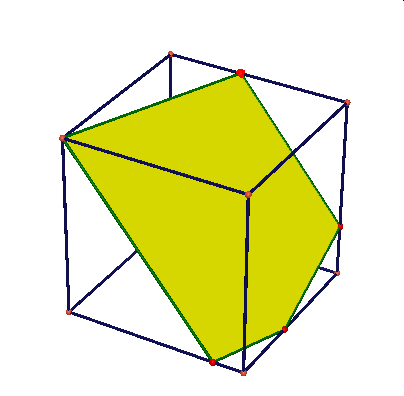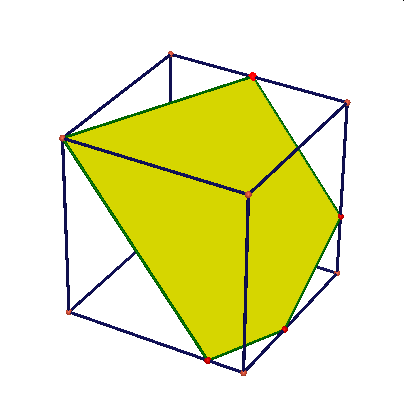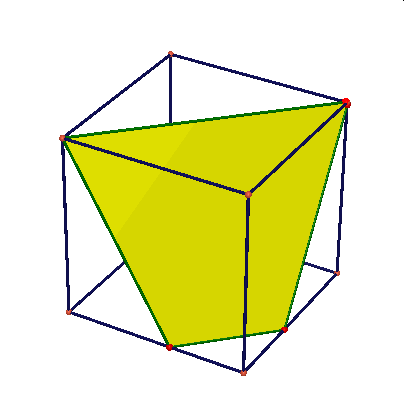
Obserwując te animacje nasuwają się liczne pytania: czy przekrojem może być dowolny trójkąt, trójkąt równoramienny, równoboczny, dowolny czworokąt, trapez, prostokąt, kwadrat, dowolny pieciokąt, pięciokąt foremny, dowolny sześciokąt, sześciokąt foremny, dlaczego nie może byc prekrojem siedmiokąt …itd.
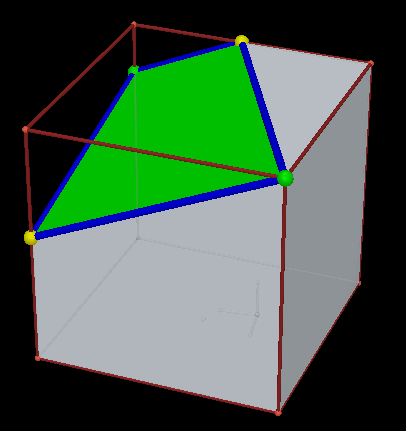
Najbardziej poularny przekrój sześcianu to przekrój płaszczyzną prostopadłą do jego głównej przekątnej. Otrzymujemy dwa rodzaje przekroju: trójkąt (dwukrotnie} lub sześciokąt.
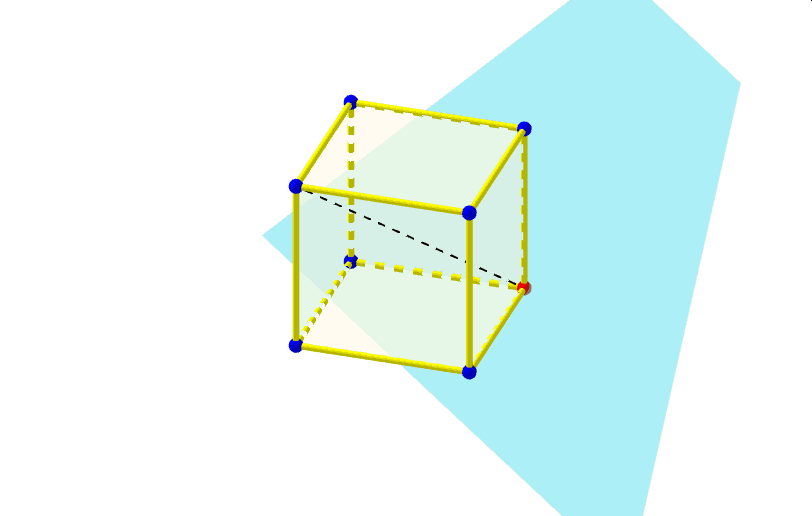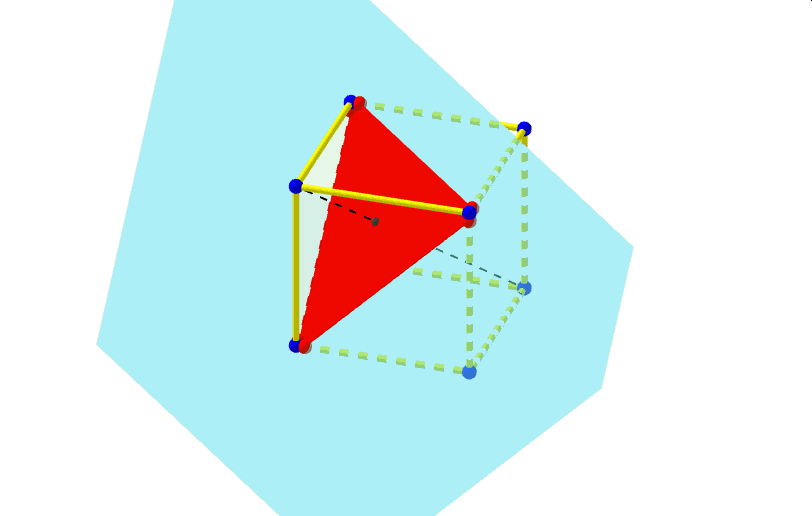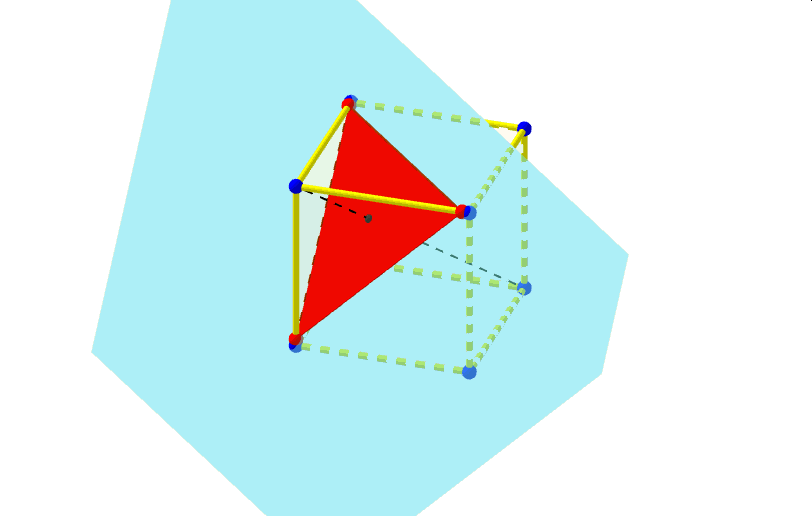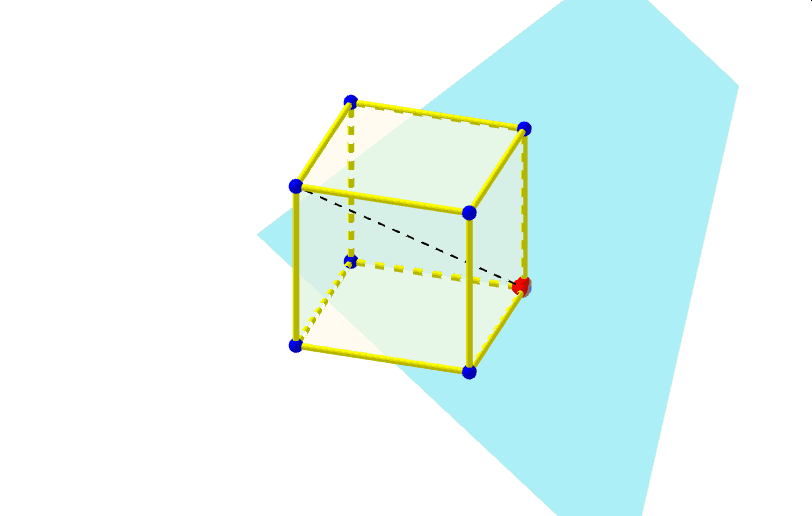
W przypadku tego przekroju warto się zastanowić, jak zmienia sie obwód tego przekroju. Poniższa animacja prezentuje taki przekrój wzbogacony dodatkowo o siatkę sześcianu, na której zaznaczone są odcinki będące bokami wielokątów tych przekrojów. Czy może się zdarzyc, że obwód przekroju sześcianu prostopadłego do jego przekątnej ma przez pewien czas stałą długość ? Jeśli się tak zdarza, to kiedy?
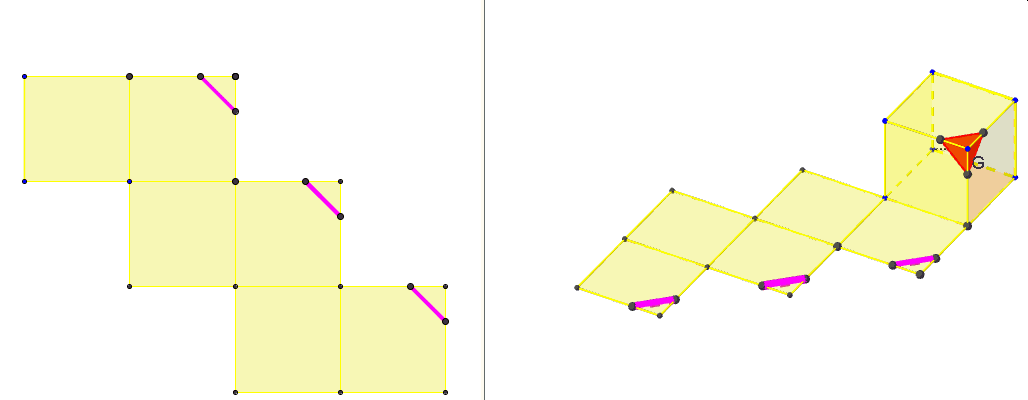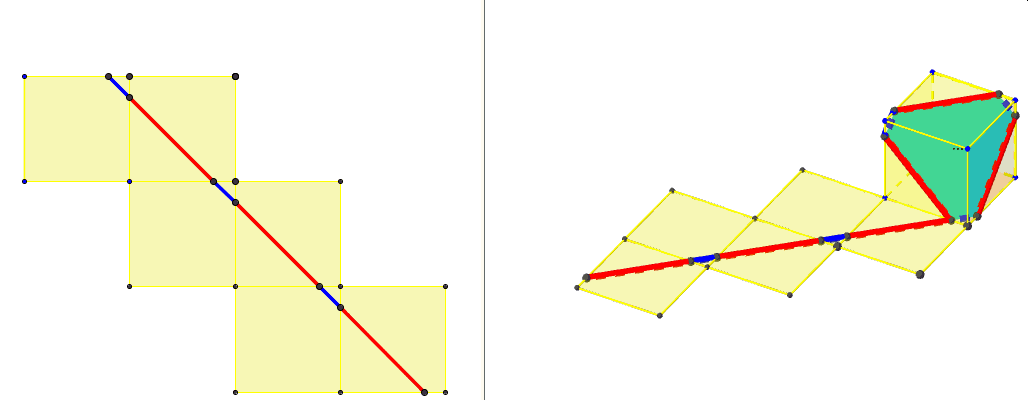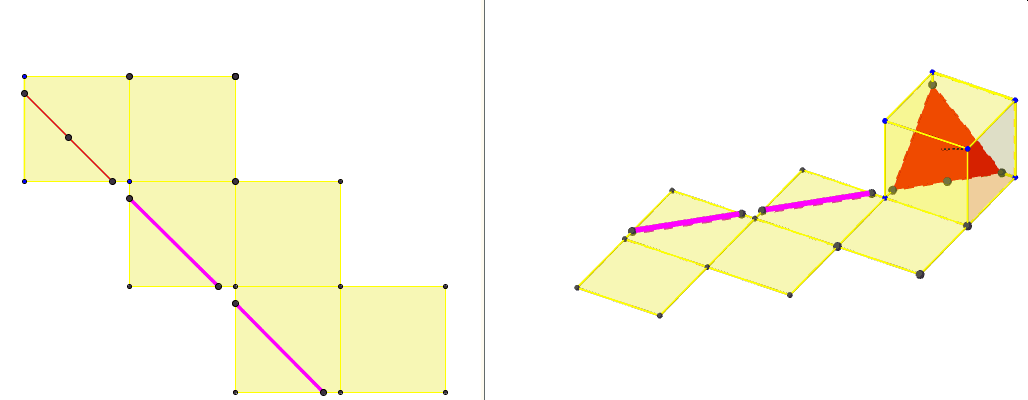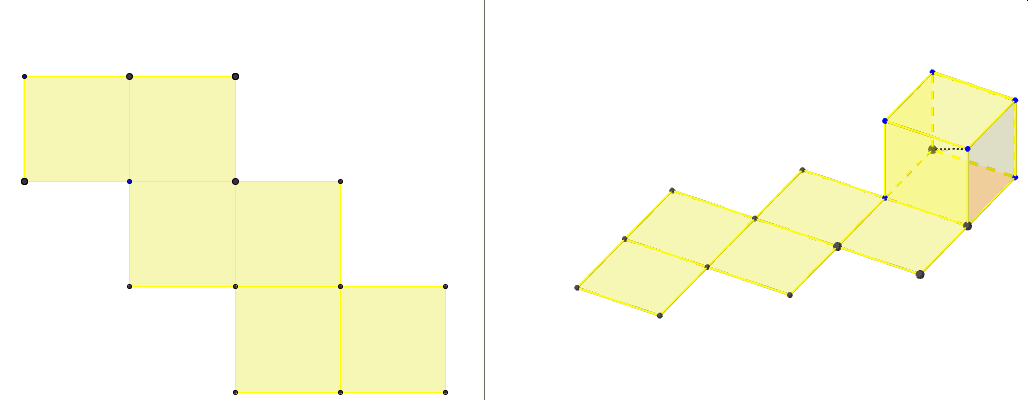
Odpowiedź na to pytanie znajdziemy w innym artykule przy zupełnie innej okazji – gdy poznamy sześcian diagonalny.
Gotowe animacje przekrojów sześcianu przypominają nam tylko, że takie istnieją.
Teraz nauczmy się konstruować przekrój szescianu w sytuacji gdy taki przekrój wyznaczony jest przez trzy zadane z góry punkty na krawędziach sześcianu? Mogą zaistnieć trzy takie sytuacje. Prześledźmy je kolejno:
Sytuacja 1
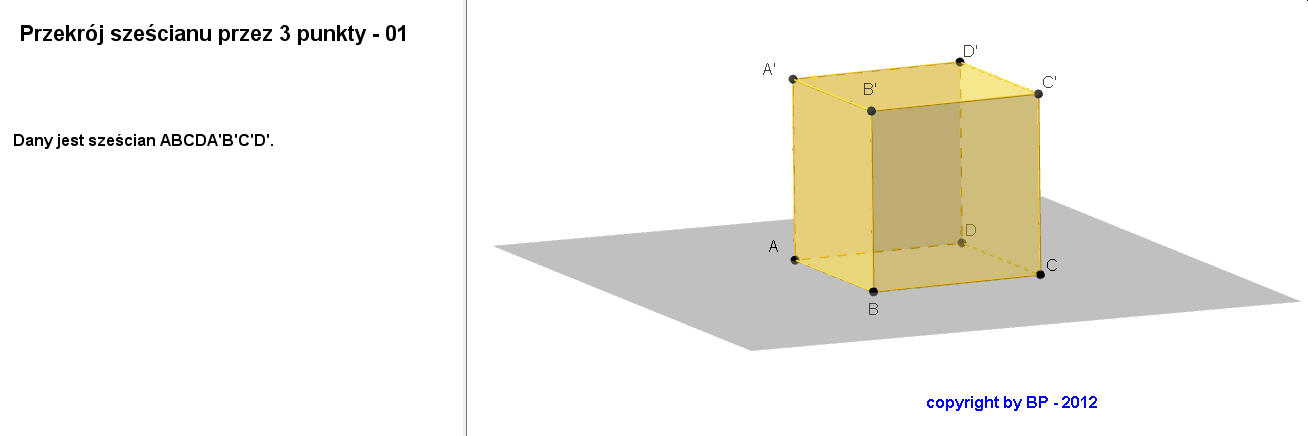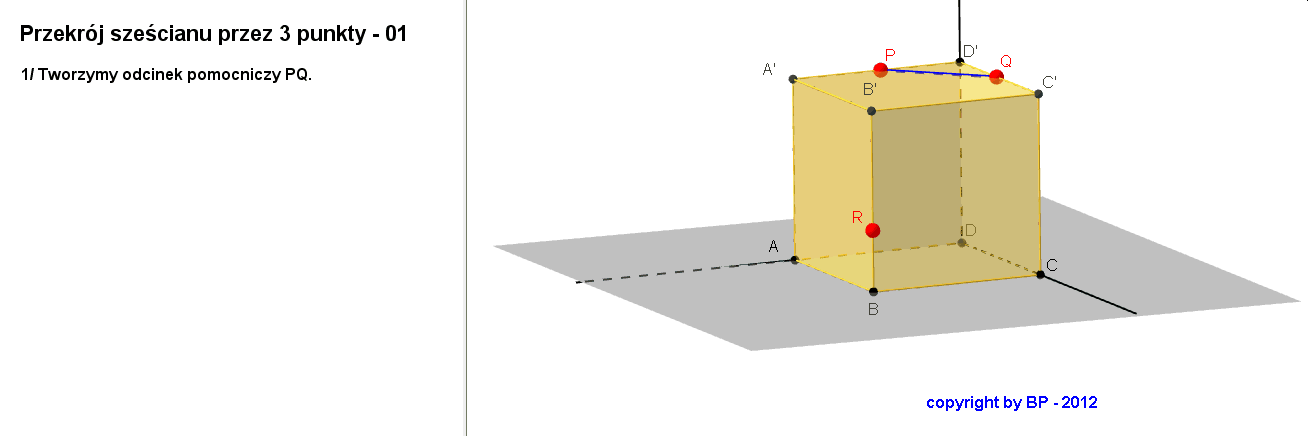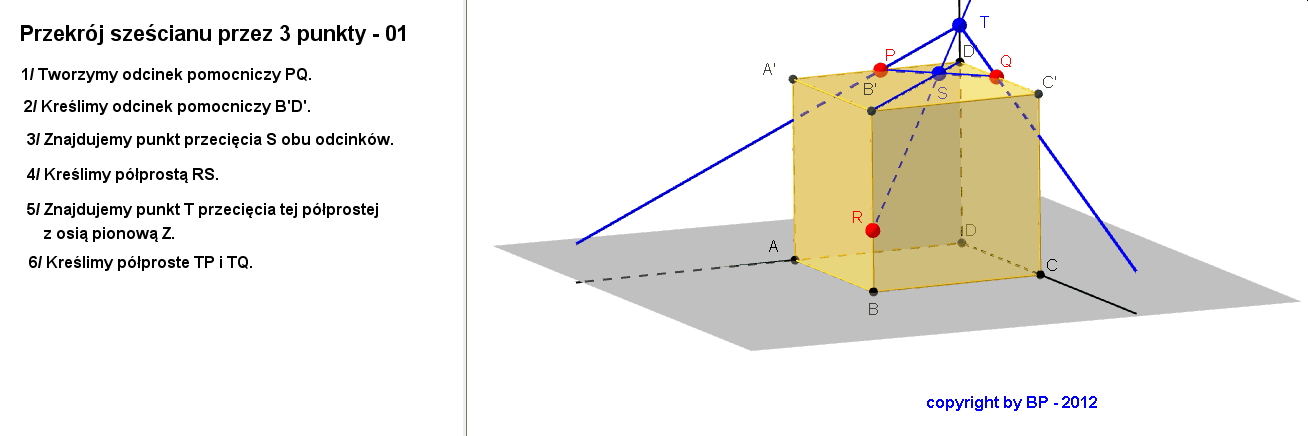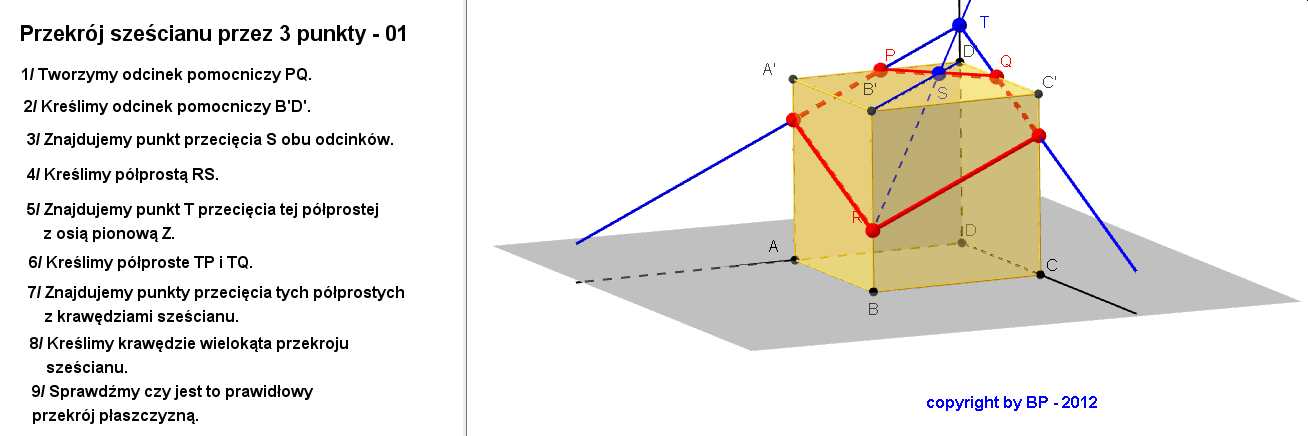
Sytuacja 2
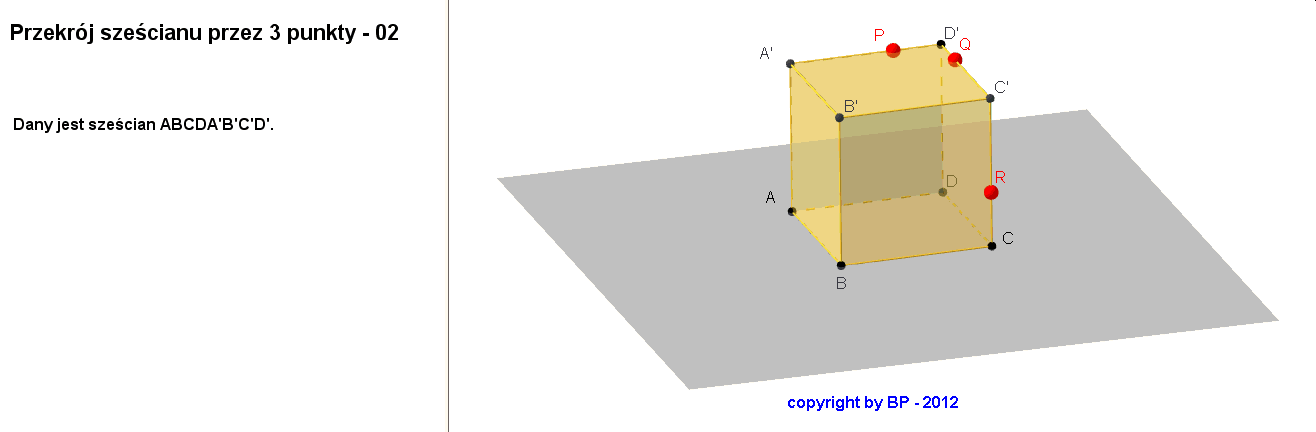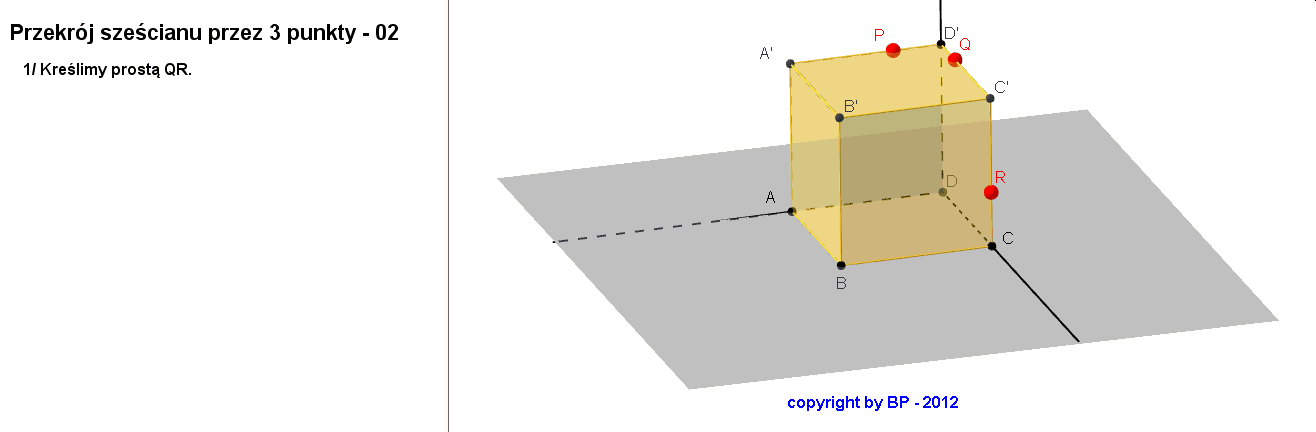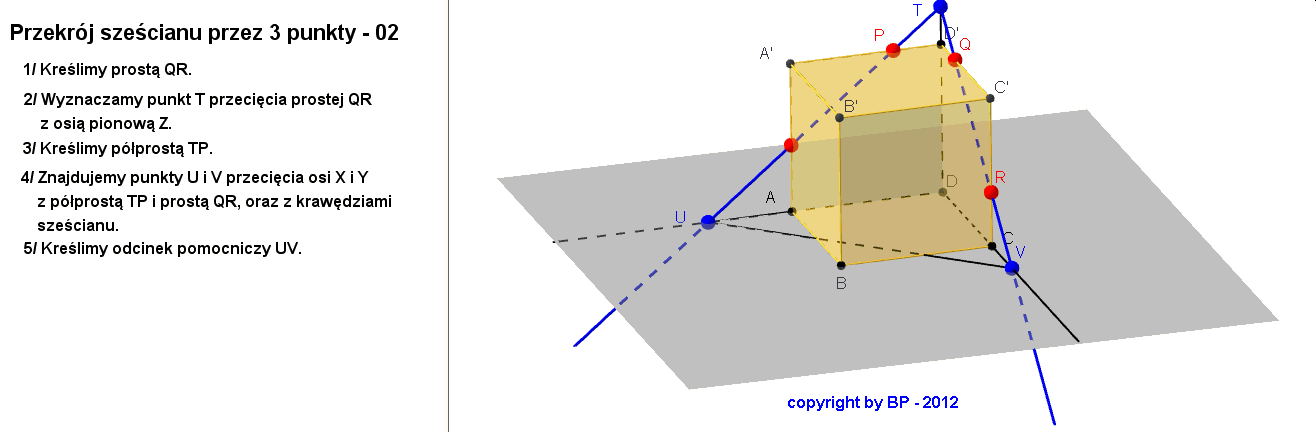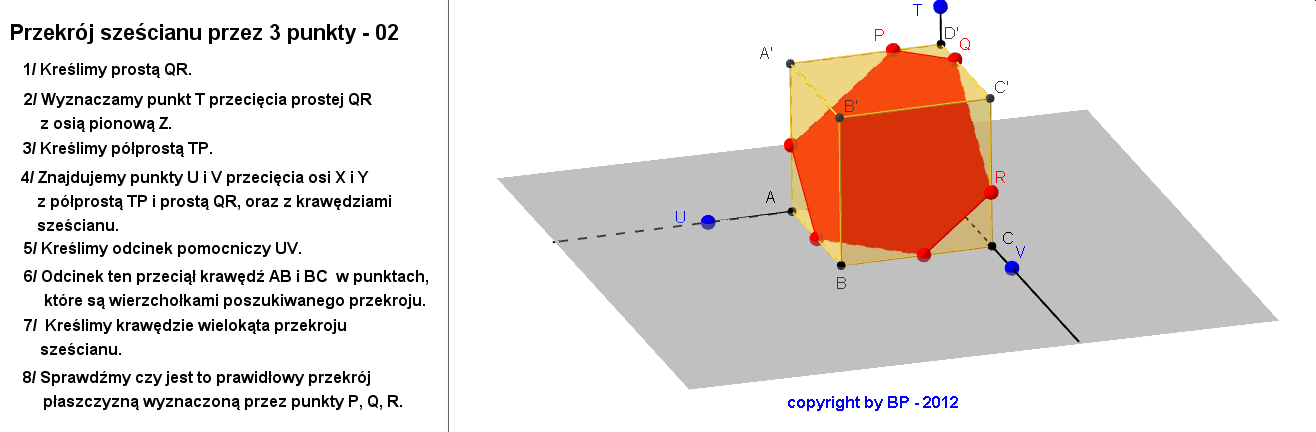
W obu tych sytuacjach co najmniej dwa z punktów P, Q, R leżały na sąsiednich krawędziach sześcianu. A co zrobić, gdy te punkty są wybrane na skośnych krawędziach sześcianu? Sytuacja troche się komplikuje.
Sytuacja 3
pojawi się wkrótce
Na koniec mały sprawdzian:
1/ Czy w takim przekroju mogą istnieć dwa boki pięciokąta tej samej długości?
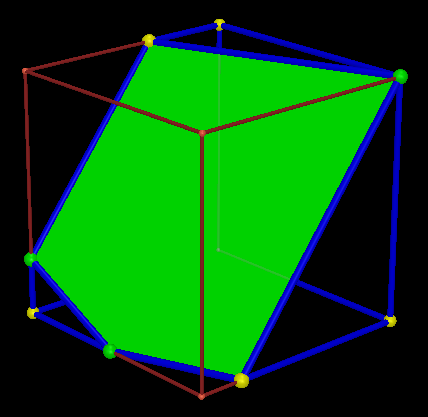
2/ Czy taki przekrój może być prostokątem?

3/ Czy ten przekrój może być dowolnym trapezem? Czy może być trapezem równoramiennym?

4/ Czy ten przekrój może mieć dwa boki tej samej długości? Czy może być wielokątem osiowosymetrycznym?
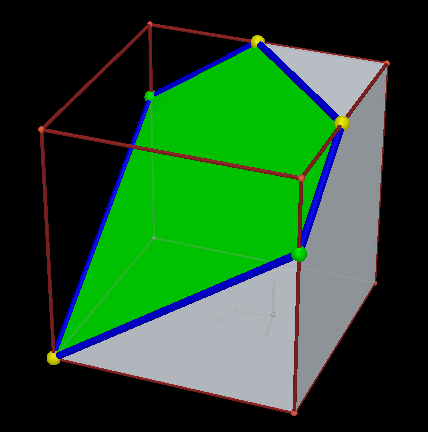
5/ A czy teraz przekrój może być osiowosymetryczny?
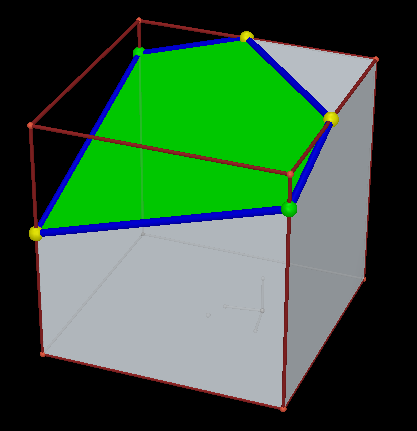
6/ Czy ten przekrój może być trapezem?
Sześcian diagonalny (diagonal position of the cube)
Słowo diagonalna oznacza „przekątną”. Sześcian diagonalny to takie ułożenie sześcianu, w którym jego jedna z przekątnych (a ile przekątnych ma sześcian?) ustawiona jest pionowo. Zauważmy, że juz trudno sobie wyobrazić takie położenie sześcianu a narysowanie jego rzutu „z pamięci” jest niemal niemożliwe. To bardzo dobre ćwiczenie kształcące wyobraźnię przestrzenną.
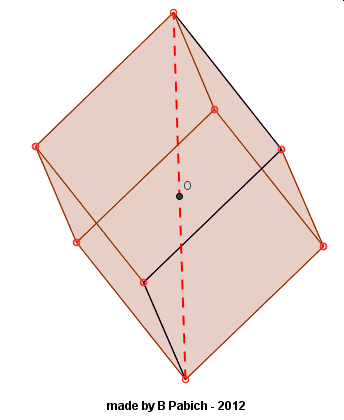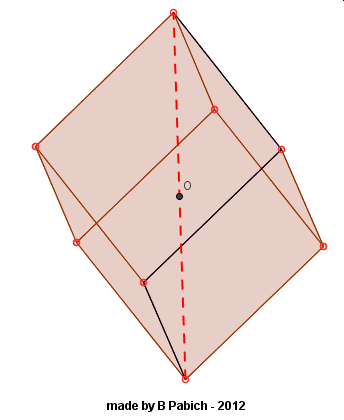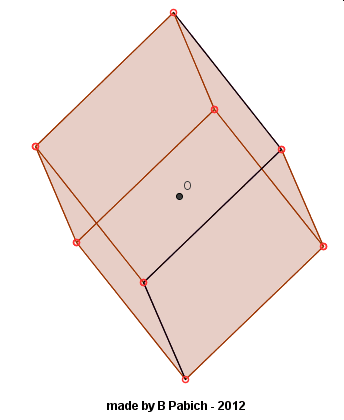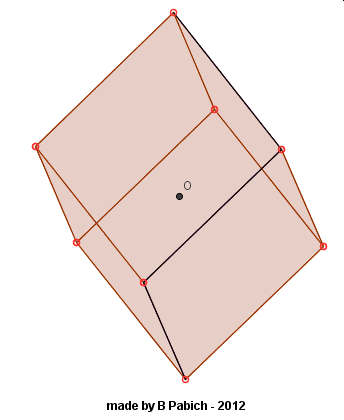
Patrząc na takie położenie sześcianu nasuwa się wiele pytań. Np. ile okręgów wykreślą wierzchołki tego sześcianu w trakcie obracania go wokół jego przekątnej? Dwa z nich pozostaną nieruchome, więc ile okręgów wykreśli sześć wierzchołków tego sześcianu? Może dwa, trzy, cztery, pięć a może sześć? No to zobaczmy:

Kolejne pytanie dotyczy krawędzi tego sześcianu. Wyobraźmy sobie, że w trakcie obracania sześcianu wokół jego przekątnej krawędzie sześcianu pozostawią ślad. Jaką bryłę obrotową otrzymamy w wyniku tego obrotu? Czy to będzie walec, stożek a może stożek ścięty, a może dwa stożki i …. , no własnie… Zobaczmy.
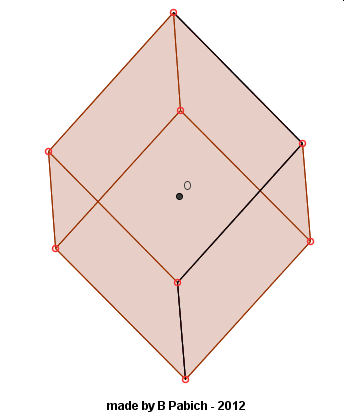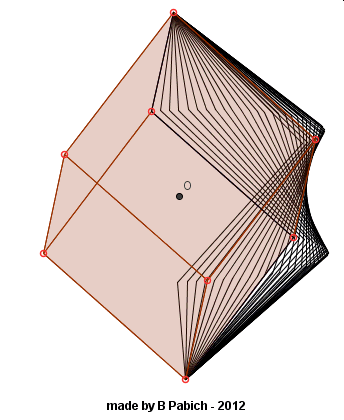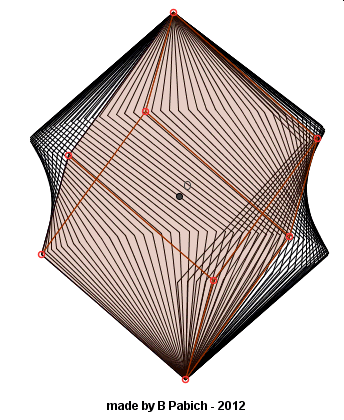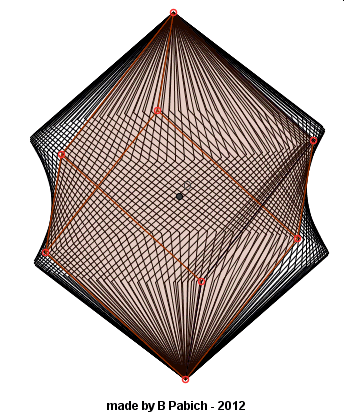
Fakt, że sześć wierzchołków sześcianu zakreśla tylko dwa okręgi, oznacza, że te wierzchołki leżą w dwóch płaszczyznach prostopadłych do osi obrotu (czyli równoległych do siebie). Nasuwa się kolejne pytanie: w jakiej odległości od siebie znajdują się te płaszczyzny? Wykreślmy trójkąty będące przekrojami sześcianu tymi płaszczyznami. Zmierzmy odpowiednie odcinki. Co widać?


Wydaje się, że punkty C i D dzielą przekątną na trzy równe odcinki. Jak udowodnić ten fakt?
Wystarczy pokazać, że wysokość BD trójkątnego ostrosłupa stanowi 1/3 długości całej przekątnej sześcianu. Oznaczmy te wysokość jako „H”. Niech długość krawędzi sześcianu jest równa „a” . Zauważmy, że objętość tego ostrosłupa możemy wyznaczyć na dwa sposoby: raz przyjmując za podstawę ostrosłupa trójkąt równoboczny o boku długości a√2 i wysokosci H, a raz przyjmując za podstawę trójkąt prostokątny o przyprostokątnych długości a i wysokości a.
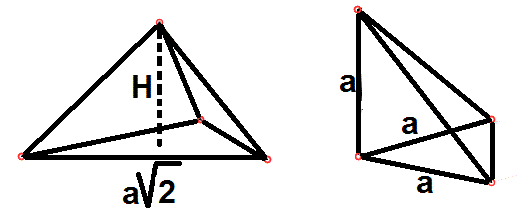
Skoro oba ostrosłupy sa przystające to ich objętosci są równe. Porównajmy je i wyznaczmy z tego równania wysokość H.
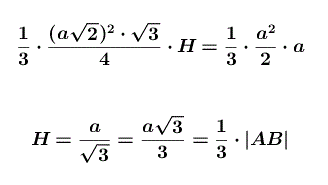 cbdu
cbdu
Kwadrat w kole a sześcian w kuli (a square in a circle and a cube in a sphere)
Nie ulega wątpliwości, że każdy z nas potrafi wpisać kwadrat w koło. Wybieramy na okręgu dowolny punkt, konstruujemy drugi punkt symetryczny do niego względem środka koła i mamy już dwa wierzchołki poszukiwanego kwadratu. Pozostałe wierzchołki łatwo już skonstruować.

Ale jak rozwiązać to zadanie analogicznie w przestrzeni 3D, czyli jak wpisać do kuli sześcian? To już nie jest takie proste. Wskazówką powinien być artykuł o sześcianie diagonalnym. Zauwżmy, że każda ze średnic kuli stanowi przekątną jednego z sześcianów wpisanych w tę kulę. Wystarczy tylko podzielić ją na trzy przystające odcinki i przez dwa ich końce poprowadzić płaszczyny prostopadłe do tej średnicy. Płaszczyzny te w przecięciu z powierzchnią kuli wyznaczą okręgi, które są opisane na dwóch trójkątach równobocznych środkowo symetrycznych względem środka sześcianu, których wierzchołki są wierzchołkami poszukiwanego sześcianu.

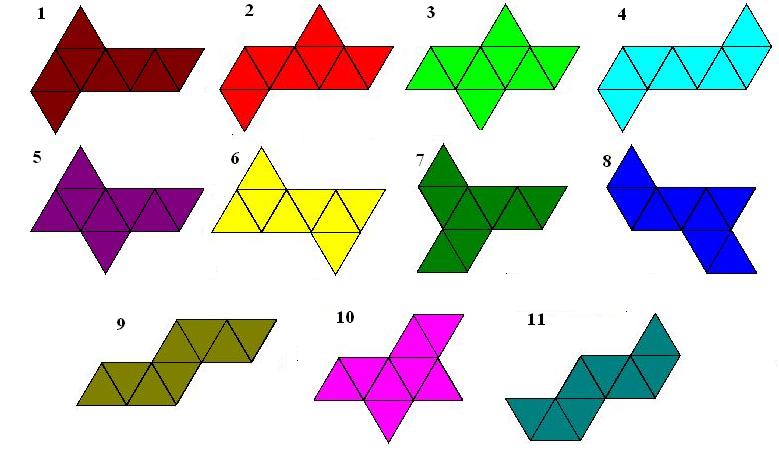
Siatki sześcianu (11 nets of cube)
Siatki sześcianu to bardzo popularny temat. Przewija się niemal przez całą edukację steeometrii. Niektórzy nawet wiedzą, że sześcian ma dokładnie 11 różnych kształtów siatki. Oto one i sposób ich tworzenia z pierwszej siatki w kształcie litery T (animacja zapożyczona z internetu z portalu Interklasa)
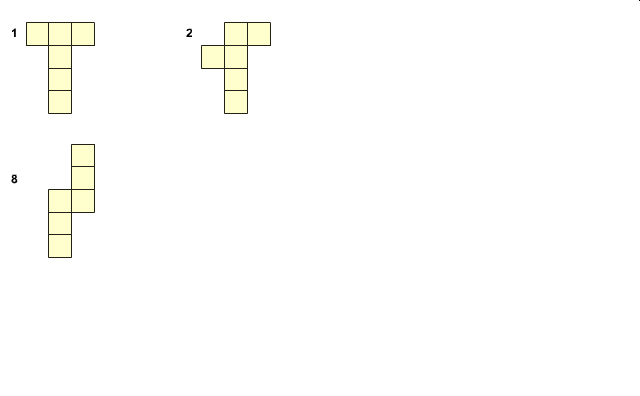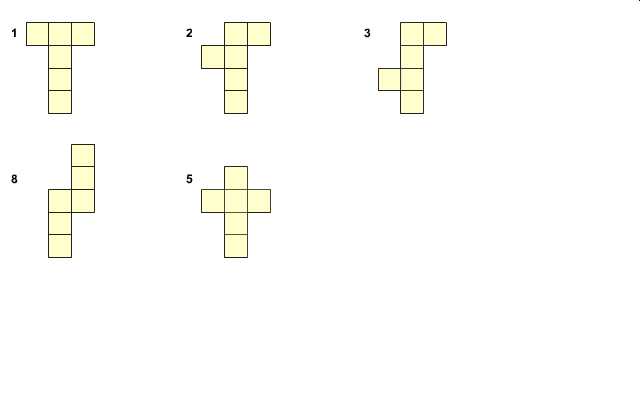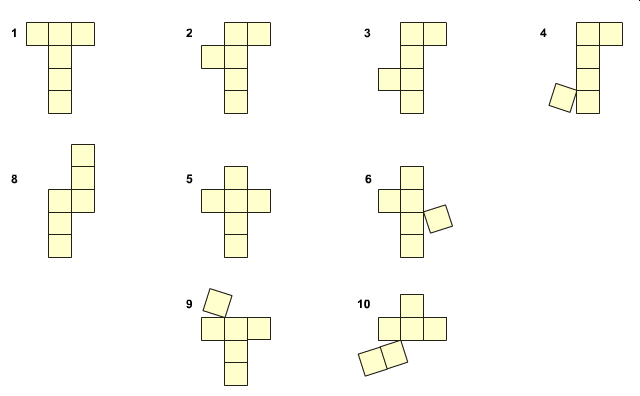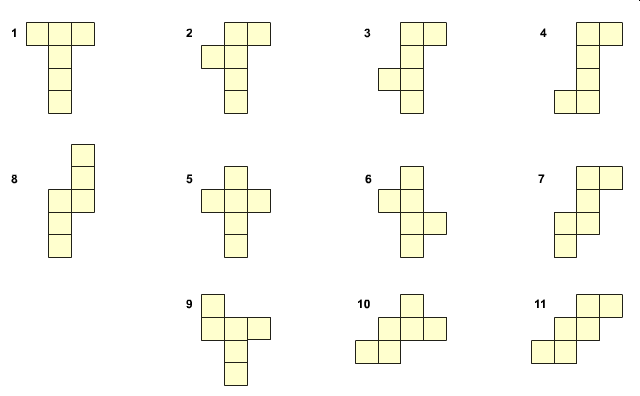
Można by się zastanowić, jak udowodnić, że jest ich dokładnie tyle. Wystarczy zastąpić każdą ścianę siatki sześcianu punktem, uzyskując tym sposobem graf takiej siatki. Na poniższym rysunku widzimy najbardziej popularną siatke w postaci „krzyża” i obok jej graf puktowy.
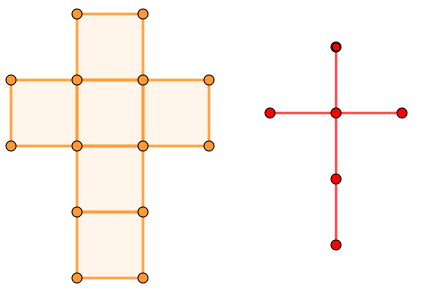
Wiadomo, że odpowiednikiem siatki nie może byc graf, w którym cztery punty znajdowałyby się obok siebie. Wówczas cztery ściany sześcianu leżałyby obok siebie, a to oznaczałoby, że żadnej z nich nie można podnieść. Taki graf siatki sześcianu nie może przyjąć kształtu litery „U”.
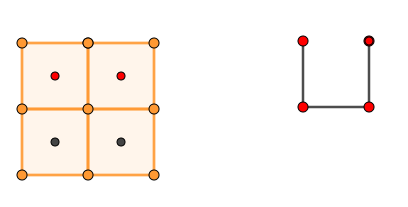
Dowód istnienia tylko 11 różnych siatek szescianu rozpoczniemy od wykreślenia grafu złożonego z jednego odcinka i będziemy tak dorysowywać kolejne pięć odcinków grafu (bo mamy ich łacznie 6, bo tyle jest ściansześcianu), by nie pojawiła się w nim litera „U”. W ten sposób wyeliminujemy wszystkie błędne sytuacje i uzyskamy tylko 11 możliwości co skończy dowód.
Siatki ośmiościanu (11 nets of octahedron)
Okazuje się że taką samą ilość siatek ma również ośmiościan foremny.
Można to wytłumaczyć faktem dualości ośmiościanu z sześcianem, czyli własnością polegającą na tym, że wierzchołki wielościanu dualnego są środkami ścian wielościanu bazowego.

O siatkach czworościanu będzie mowa w artykule „Czworościan foremny”.
Natomiast ciekawostką jest fakt, że dwunastościan foremny i jego dualny „przyjaciel” – dwudziestościan foremny mają też taką samą liczbę siatek co dualne ze sobą sześcian i ośmościan i wynosi ona aż 43380