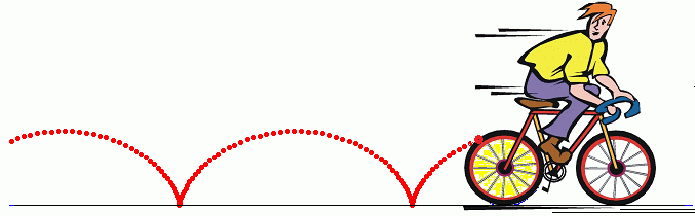
Słowo „cykloida” pochodzi od greckiego kuklos ( κύκλος ) oznaczającego „pierścień” lub „okrąg”. Wyobraźmy sobie koło (na przykład  roweru) toczące się bez poślizgu po prostej. Punkt należący do brzegu takiego koła toczącego się po linii prostej wykreśla krzywą zwaną cykloidą. Popatrzmy na to w sposób dynamiczny:

Jeśli z tym kołem zwiążemy inny punkt – np. należący do wnętrza tego koła, to mamy do czynienia z cykloidą skróconą…

… a w przypadku punktu leżącego poza tym kołem – z cykloidą wydłużoną.

Na pewno niejeden użytkownik programu Cabri II Plus lub GeoGebry zapragnąłby samodzielnie skontruowac takie obracające się koło wraz z cykloidą. Oto dynamiczny opis takiej konstrukcji:

Wynikiem końcowym tej konstrukcji jest punkt P. Poruszając punktem M po prostej powodujemy obracanie się skonstruowanego koła zaś ślad punktu P wykreśli cykloidę.

Punkt P wyznacza punkt okręgu, który obracamy poruszając punktem M po półprostej.
Dlaczego musieliśmy zmienić miarę długości odcinka AM na ujemną?
Dlatego, że odmierzanie punktu Q na okręgu o środku S i promieniu SM odbywa się w kierunku ujemnym (zgodnym ze wskazówkami zegara), a dynamiczne programy komputerowe rozróżniają obieg dodatni i ujemny.
Wybór punktu P na półprostej SQ decyduje o tym, czy cykloida będzie zwykła, wydłużona czy skrócona.
Aby zmienić rodzaj cykloidy, zmieniamy tylko położenie punktu P na półprostej SQ.

POLE POD CYKLOIDĄ  (area under the cycloid – method of Torricelli

Już w XVI wieku matematycy zajmowali się wyznaczaniem pola obszaru znajdującego się pod cykloidą.
We Włoszech próbowali tego Galileo Galilei (1564-1642), Evangelista Torriceli (1608-1647) i Bonaventura Cavalieri (1598-1647), we Francji Martin Mersenne (1588-1648), Gilles de Roberval (1602-1675), Blais Pascal (1623-1662) i Rene Descartes (Kartezjusz) (1591-1661). Zarówno Torricelli jak i Cavalierii byli uczniami Galileusza.

Cavalieri sformułował zasadę, znaną już w Starożytności Archimedesowi, w myśl której pola dwóch  obszarów są sobie równe, jeśli wszystkie odcinki przekroju tych obszarów prostą należącą do ustalonego kierunku mają tę samą długość na tej samej wysokości tego obszaru. Popatrzmy na poniższą dynamiczną prezentację:

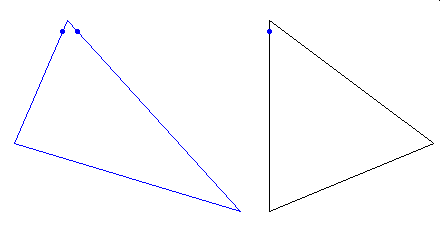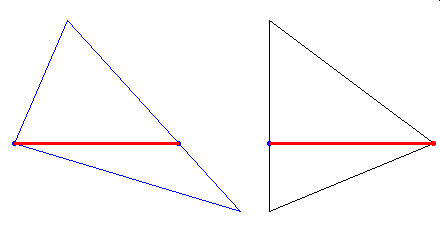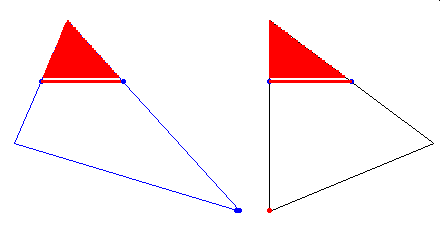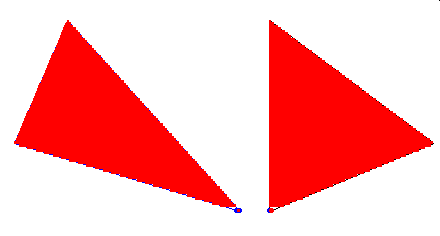
Widzimy na niej dwa różne trójkąty. Odcinki poziome poprowadzone w obu trójkatach mają na każdym poziomie wysokości tę samą długość. Według zasady Archimedesa-Cavalieriego oba trójkąty mają takie samo pole.

Mimo że Cavalieri znał tę zasadę, nie potrafił wykorzystać jej w wyznaczeniu pola obszaru pod cykloidą.
Zmierzył to pole metodą doświadczalną: Wyciął z jednolitego kawałka drewna obszar pod cykloidą, oraz koła tworzącego cykloidę i zważył oba kawałki na wadze. Okazało się wówczas, że drewniany obszar pod cykloidą „waży” niemal trzykrotnie więcej niż toczące się drewniane koło wykreślające swym punktem cykloidę. Dopiero Torricelli przeprowadził dowód tego faktu metodą, którą dziś nazwalibyśmy dowodem „przez ogląd”. Po jego dokładnym przeanalizowaniu okazuje się, że Cavalierii nie popełnił błędu w „ważeniu” pól figur.
Spróbujmy prześledzić rozumowanie Torricelliego przy pomocy współczesnego narzędzia, jakim jest komputer. Program CABRI lub GeoGebra pozwala przybliżyć jego eksperyment poprzez dynamiczną konstrukcję, w której odpowiednie manipulowanie obiektami pozwala zamienić obszar pod cykloidą na równoważny i bardziej znany inny obszar, ułatwiając tym samym wyznaczenie jego pola.

Zauważmy, że obszar pod cykloidą składa się z trzech segmentów – dwóch przystających obszarów (1) i (3) (koloru zielonego) oraz obszaru (2) – koła,  które wygenerowało tę cykloidę.
By udowodnić, że obszar pod cykloidą to 3 pola koła, wystarczy wykazać, że każdy z obszarów (1) oraz (3) ma pole równe polu koła bazowego (2).

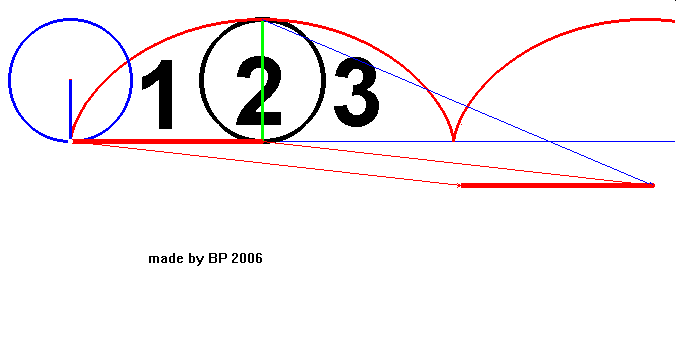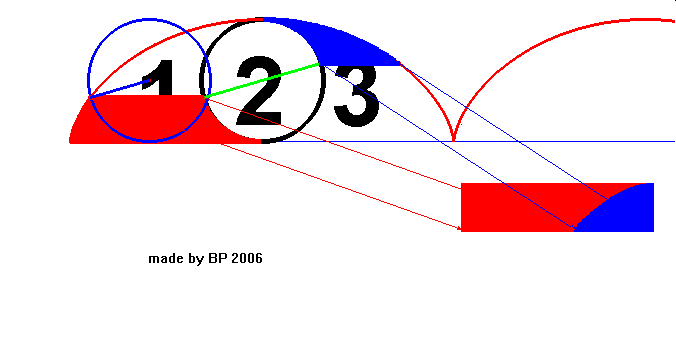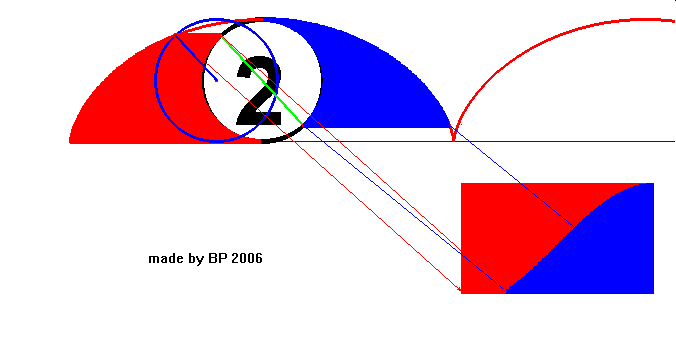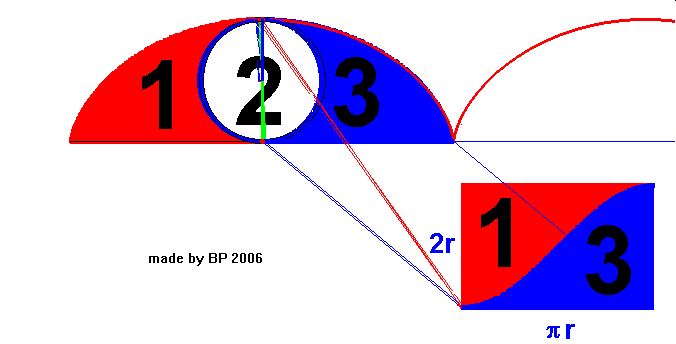
Eksperyment polega na zsumowaniu wszystkich par odcinków równoległych do prostej pod cykloidą, których jeden koniec leży na łuku cykloidy, a drugi na okręgu (2). Jeden odcinek każdej pary należy do obszaru (1), drugi do obszaru (3). Okazuje się, że wszystkie te odcinki składają się w sumie na prostokąt o wymiarach 2r · πr = 2πr², czyli jego pole jest równe dwóm polom koła, co kończy dowód.

ODWRÓCENIE CYKLOIDY – BRACHISTOCHRONA ( brachistochrone curve as inverse of cycloid)

Gdy cykloidę odwrócimy „do góry nogami„, wówczas otrzymamy krzywą, która stałą się przyczynkiem do powstania nowej dziedziny matematyki – rachunku wariacyjnego. Okazuje się bowiem, że jeśli tak odwróconą cykloidę umieścimy między dwoma punktami A i B tak jak na poniższej animacji, wówczas kulka o masie m będzie staczać się po tej krzywej najszybciej z wszystkich kul o tej samej masie , które toczą sie po innych krzywych zawartych między A i B. Tak odwrócona cykloida nosi nazwę brachistochrony czyli krzywej najszybszego spadku. WS naszym przypadku brahistochrone prezentuje krzywa koloru czerwonego. Dwie pozostałe krzywe to parabola (zielona) i prosta (niebieska). Uruchamiamy przyciskiem animcje trzech kul i obserwujemy która z nich najszybciej dociera do celu.

HIPOCYKLOIDY I EPICYKLOIDY (Hipercycloids and Epicycloids)

Punkt należący do brzegu koła toczącego się wewnątrz innego koła wykreśla krzywą zwaną hipocykloidą. Podobnie jak dla cykloidy możemy uzyskać hipocykloidę zwykłą, skróconą lub wydłużoną.

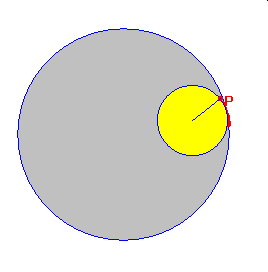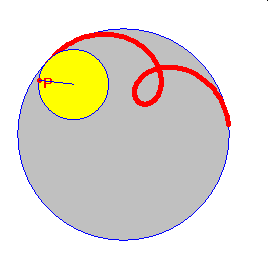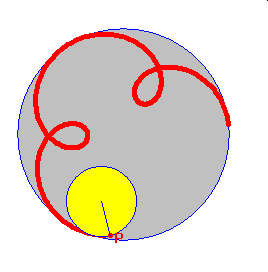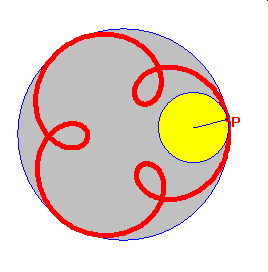
hipocykloida zwykła                                  hipocykloida skrócona                                hipocykloida wydłużona

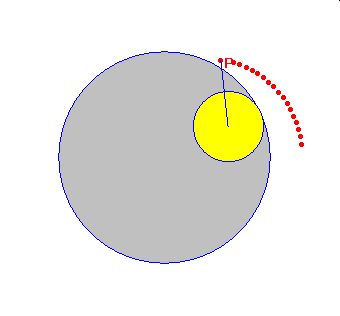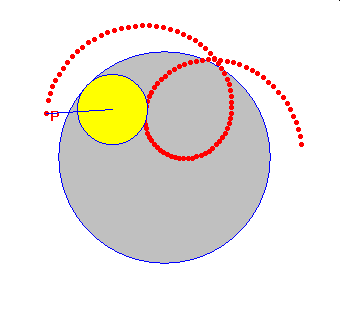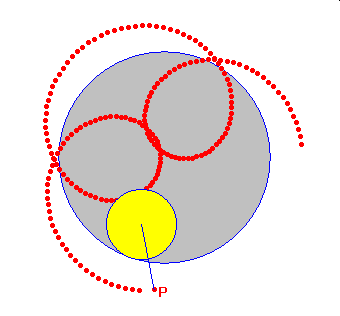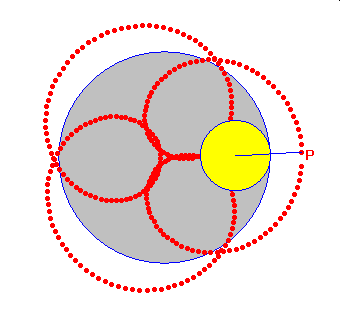
Dla tych którzy chcieliby samodzielnie skonstruować hipocykloidę w programie Cabri lub w GeoGebrze zamieszczono poniżej szkic tej konstrukcji.

 

 

 

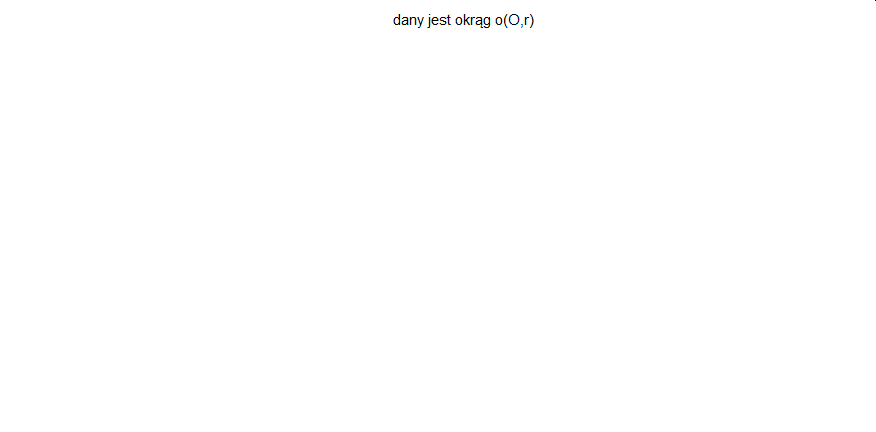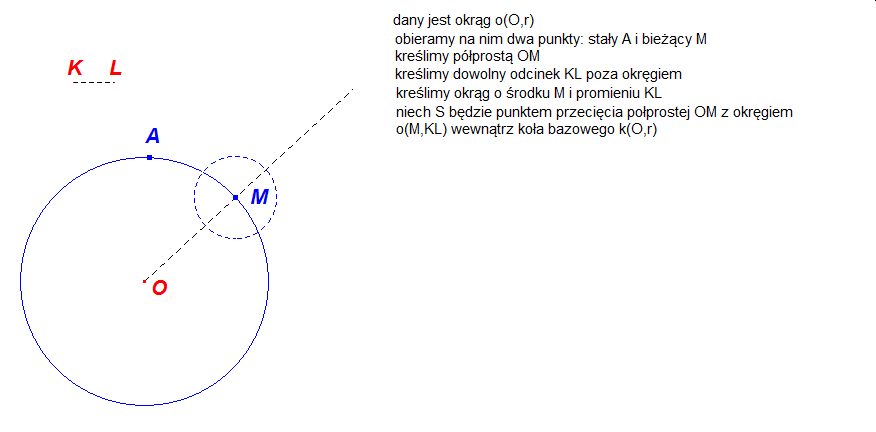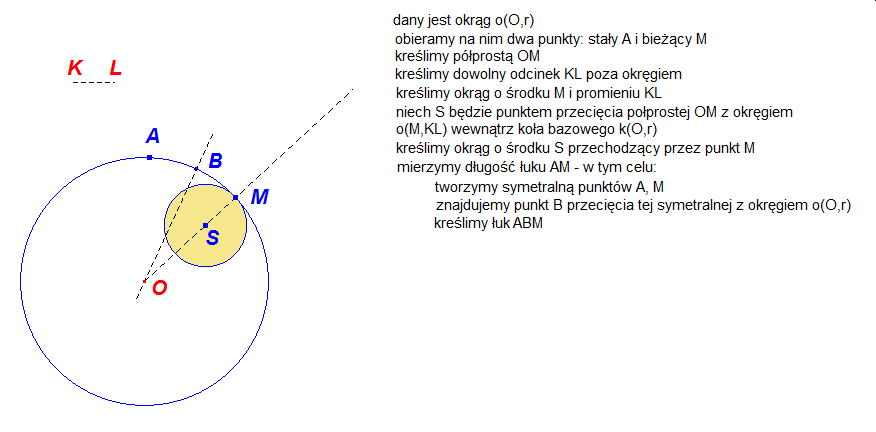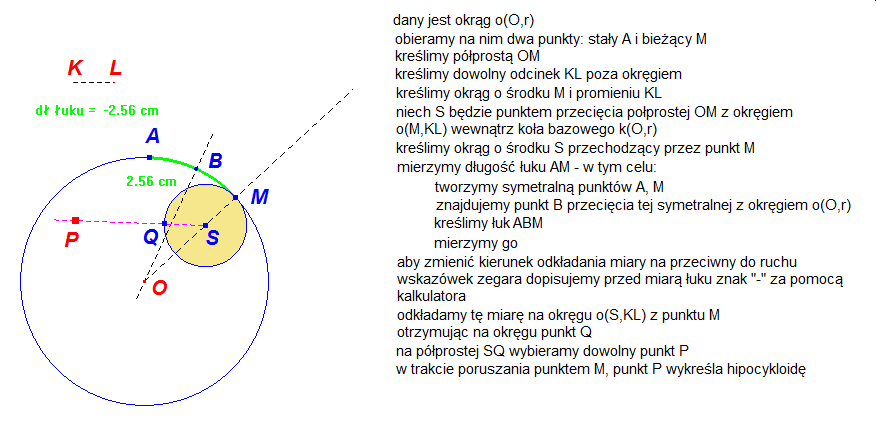
Punkt  należący do brzegu koła toczącego się na zewnątrz innego wykreśla epicykloidę. I znowu analogicznie można uzyskać epicykloidę zwykłą,skróconą lub wydłużoną.

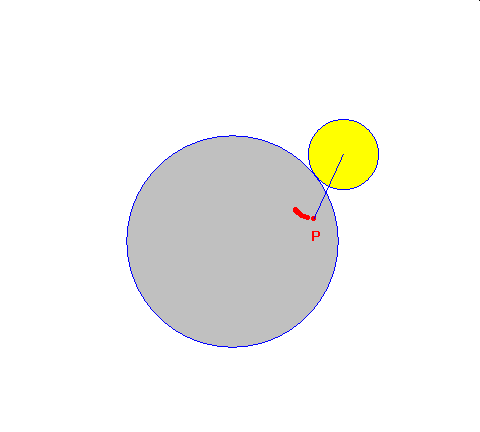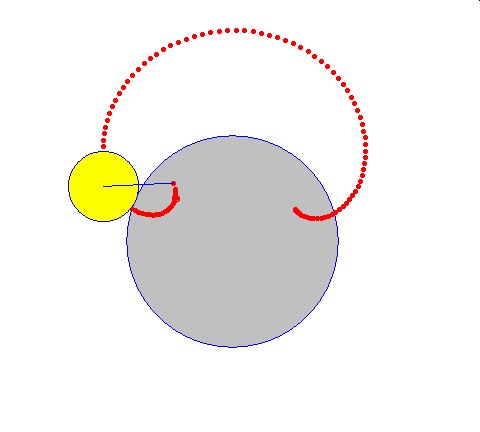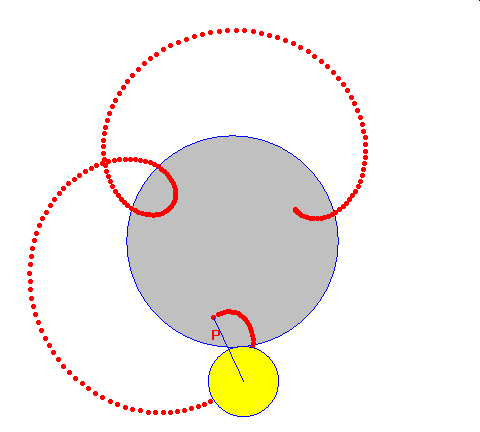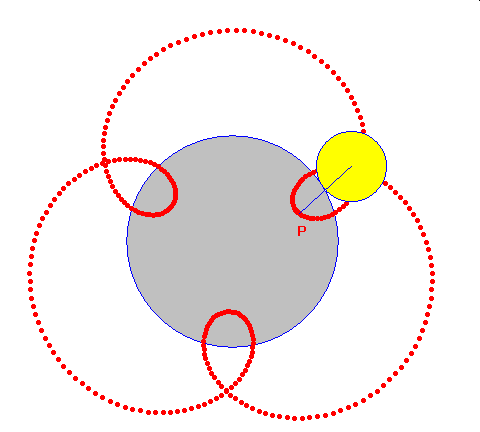
epicykloida zwykła                                    epicykloida skrócona                               epicykloida wydłużona

Czy z dynamicnej ilustracji hipocykloidy można wywnioskować ile razy promień większego okręgu jest większy od promienia mniejszego?
Dla tych którzy chcieliby samodzielnie skonstruować epicykloidę w programie Cabri lub w GeoGebrze zamieszczono poniżej szkic tej konstrukcji.

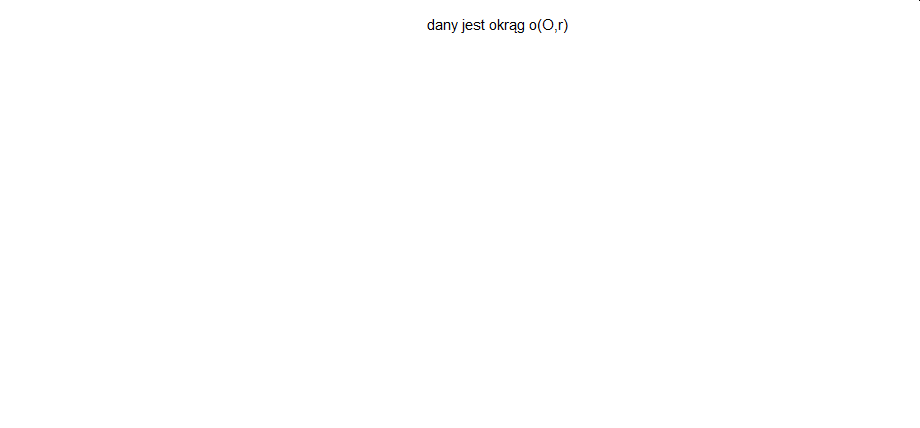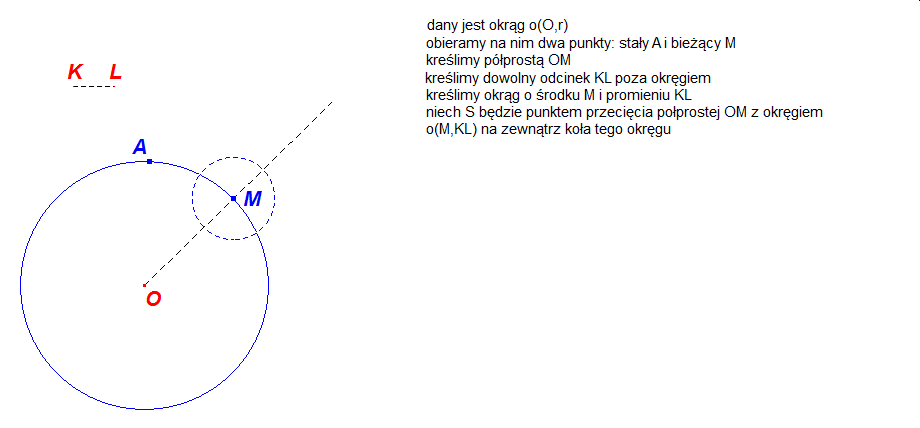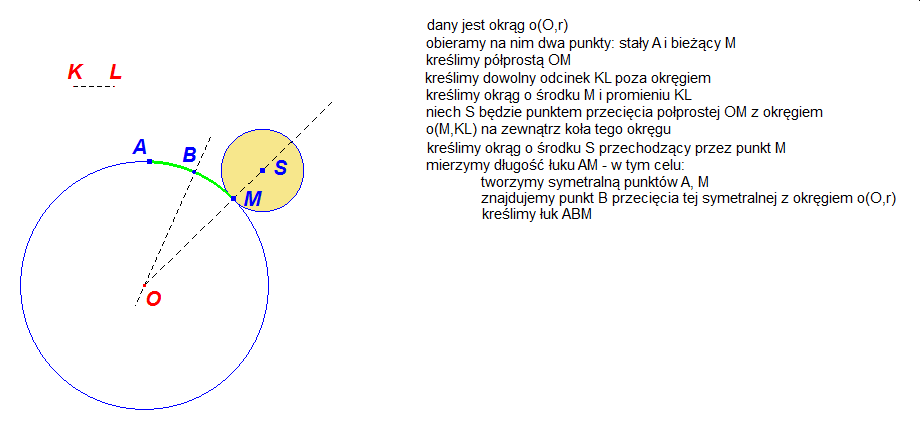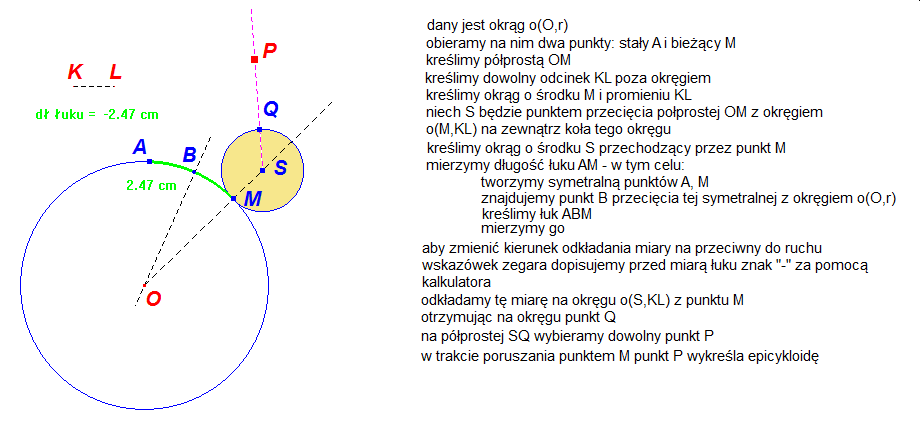
W obu powyższych konstrukcjach P wyznacza punkt, który wykreśla trajektorię, gdy obracamy punktem M po okręgu bazowym. Wybór punktu P na półprostej SQ decyduje o tym, czy hipo/epi cykloida będzie zwykła, wydłużona czy skrócona.
Dlaczego musieliśmy zmienić miarę długości odcinka AM na ujemną, skoro miara jest zawsze dodatnia?
Dlatego, że ruch punktu Q na okręgu o środku S odbywa się w kierunku zgodnym ze wskazówkami zegara, a w matematyce miara kąta obrotu w tym kierunku jest ujemna, a kąt nazywamy ujemnie skierowany.
Zwróćmy uwagę, że kształt hipocykloidy i epicykloidy skróconej przypomina pewien element architektury gotyckiej, zwany maskwerkiem.
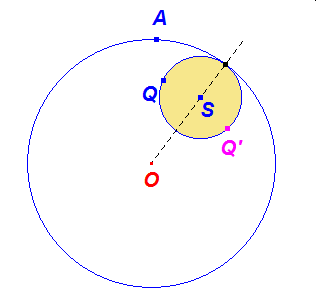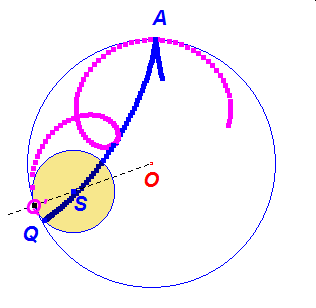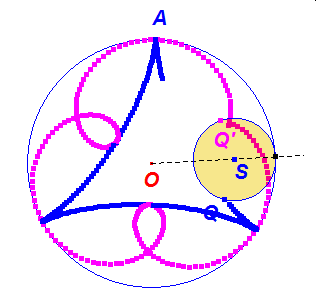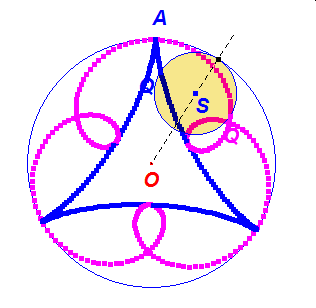
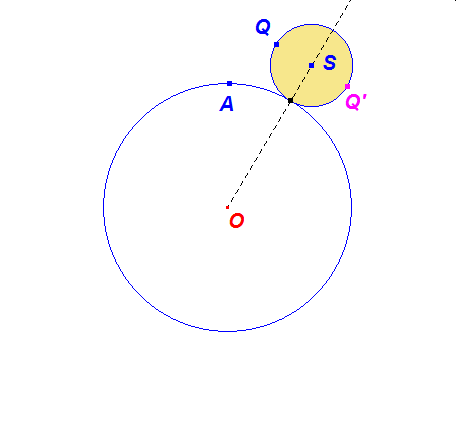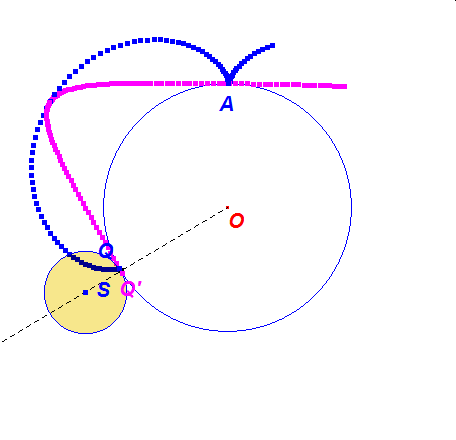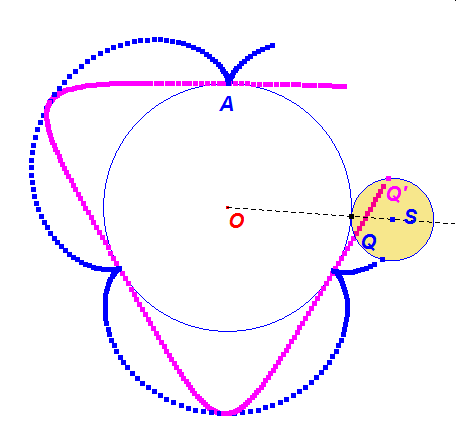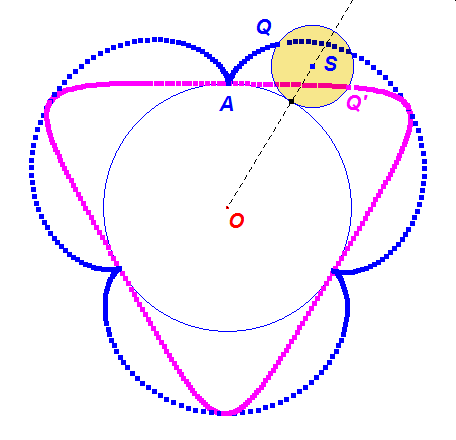
Zobaczmy, co się stanie gdy w przypadku hipo i epicykloidy zwykłej, odbijemy punkt Q w symetrii osiowej względem półprostej OM, uzyskując punkt Q’.
Ruch punktu Q’ po okręgu o(S,KL) będzie wówczas przeciwnie skierowany do ruchu punktu Q na tym okręgu. A jak zachowują się trajektorie obu punktów? Czy punkty ich zetknięć to przypadek? Popatrzmy na dynamiczną ilustrację tego faktu.

HIPOCYKLOIDY I EPICYKLOIDY NIECO INACZEJ (a different look at the hypocycloide and epicykloide)

Wykonajmy pewne doświadczenie: wyobraźmy sobie, że po dwóch okręgach poruszają się dwa punkty obracając się wokół środka każdego z nich z różnymi prędkościami w tych samych, lub  przeciwnych kierunkach.
Co wykreśli wówczas środek odcinka łączącego te dwa punkty?

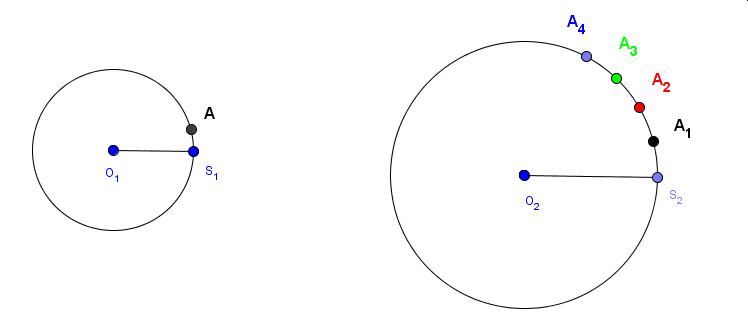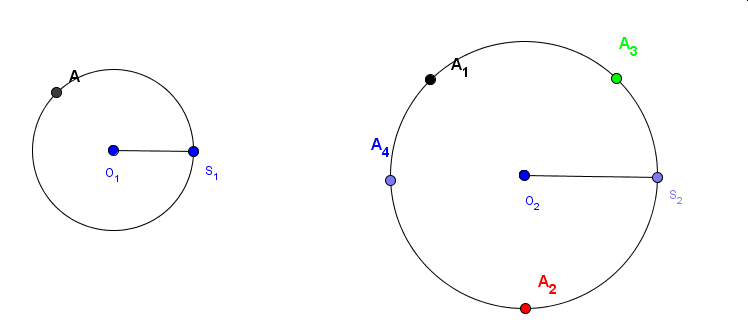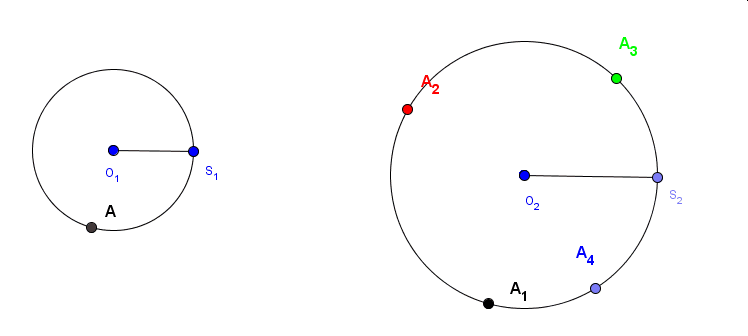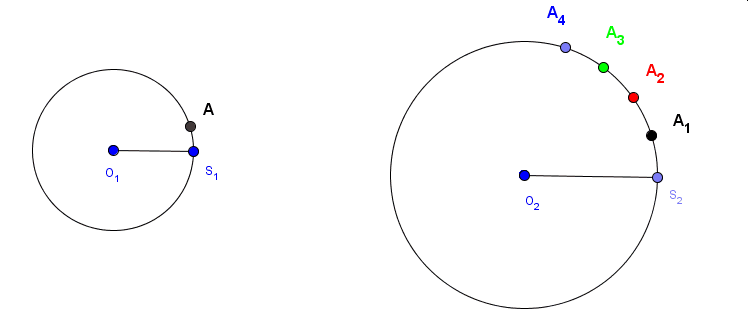
Popatrzmy najpierw na poniższą animację.Animacja dokonuje sie dzieki poruszaniu pnktem A1. Widać na niej, że punkty A i A1 poruszają się z tą samą prędkością. Natomiast punkty A2, A3 i A 4 poruszają sie odpowiednio dwukrotnie, trzykrotnie i czterokrotnie szybciej w tym samym kierunku. .Wynika to z faktu,że |∠S2O2A2| = 2· |∠S2O2A2| ,  |∠S2O2A2| = 3· |∠S2O2A3| oraz  |∠S2O2A2| = 4· |∠S2O2A4|.

Teraz utwórzmy środki odcinków AA2, AA3 i AA4 zaznaczone odpowiednimi kolorami i obserwujmy krzywe, jakie zakreślą te punkty w trakcie ruchu punktu A1.

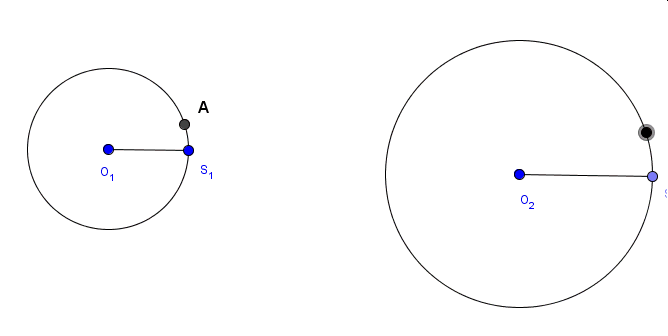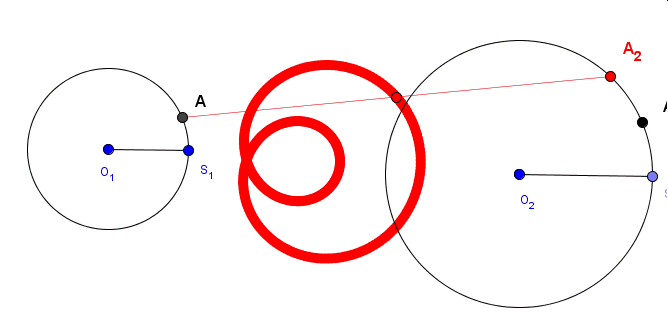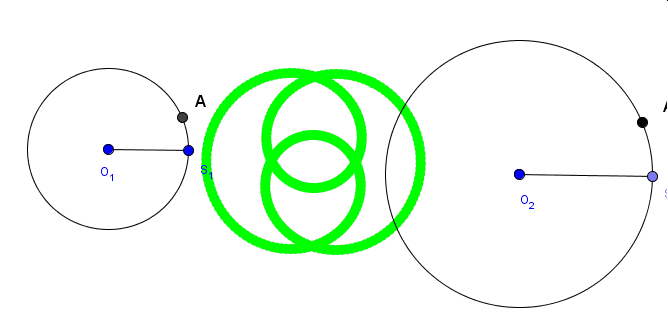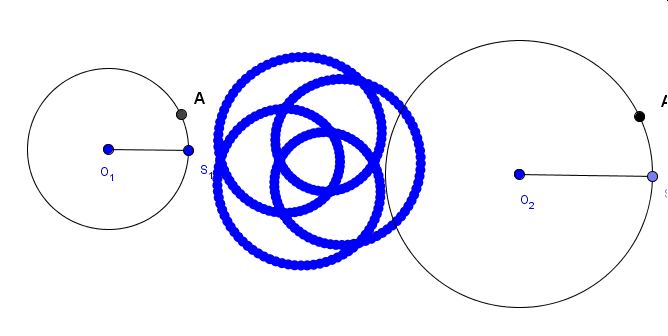
A co się stanie, gdy punkt A1 będzie się poruszał przeciwnie niż punkt A? Zobaczmy…..

WYSZYWANKI MATEMATYCZNE (mathematical stiching)

Mówiąc o toczeniu się kół wewnątrz innych kół nie sposób pominąć tematu „Wyszywanki”, który znają już uczniowie klas Szkoły Podstawowej. Aby „wejść” w temat wykonajmy pewne doświadczenie.

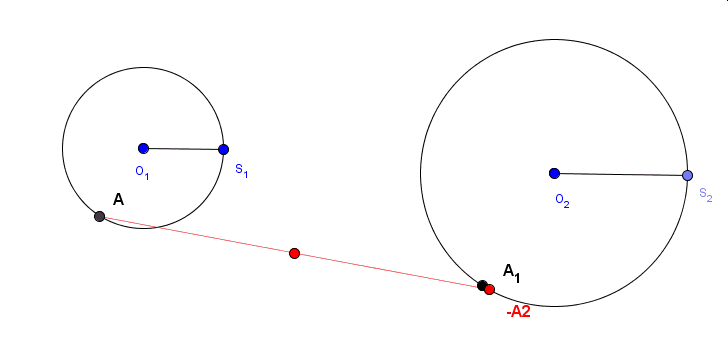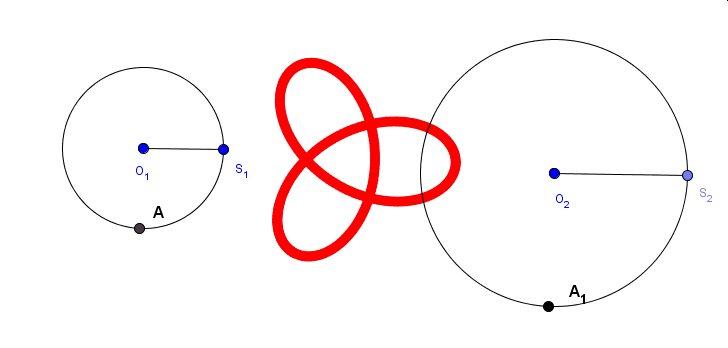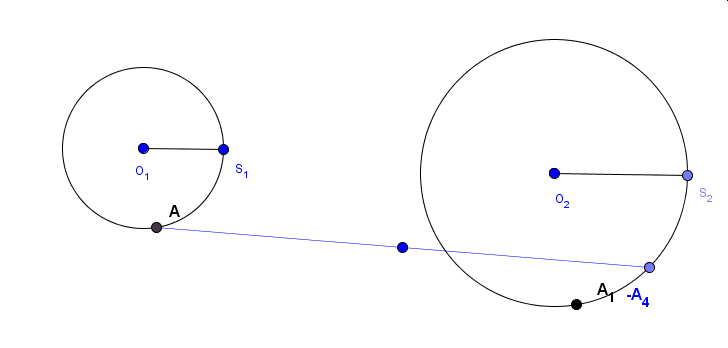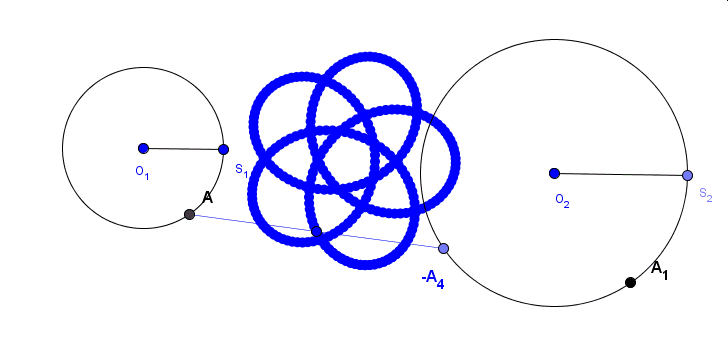
Wyobraźmy sobie, że po okręgu poruszają się dwa punkty z różnymi prędkościami obracając się wokół środka w  przeciwnych kierunkach. Co wykreśli wówczas odcinek łączący te dwa punkty?

 

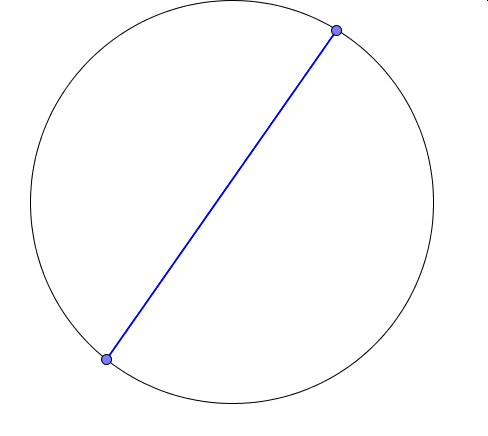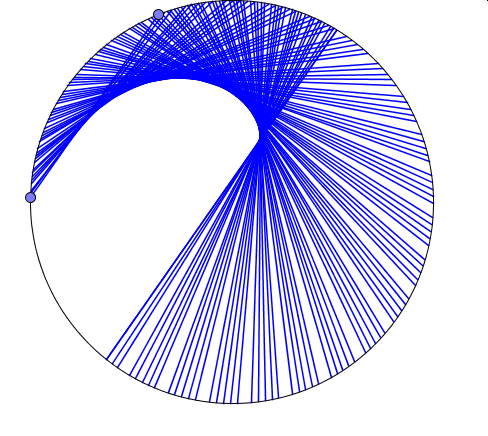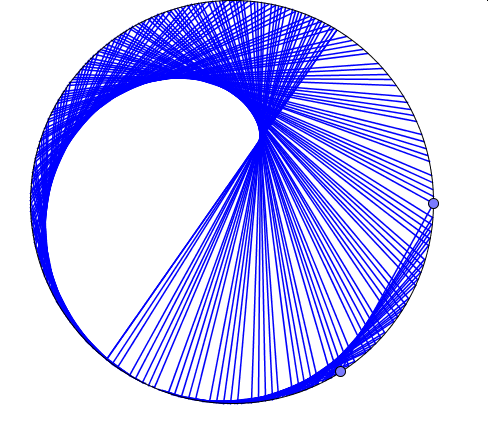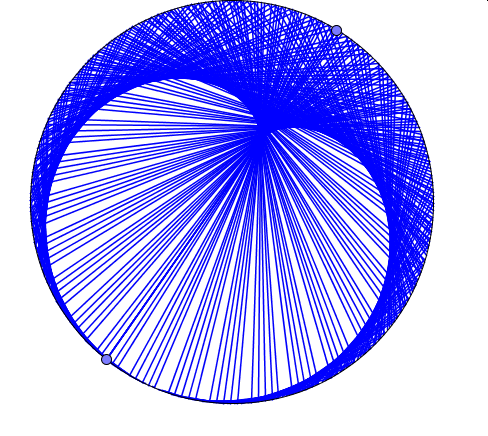
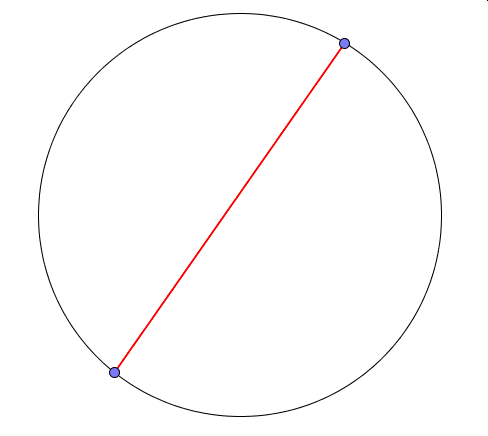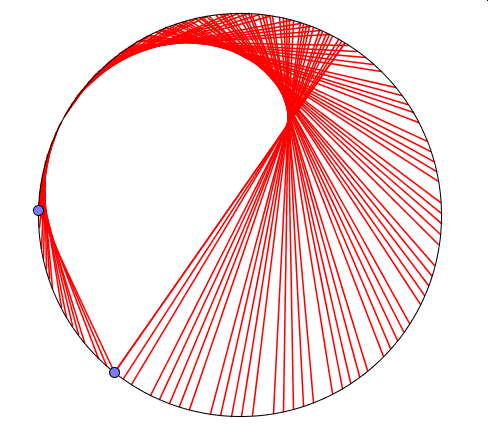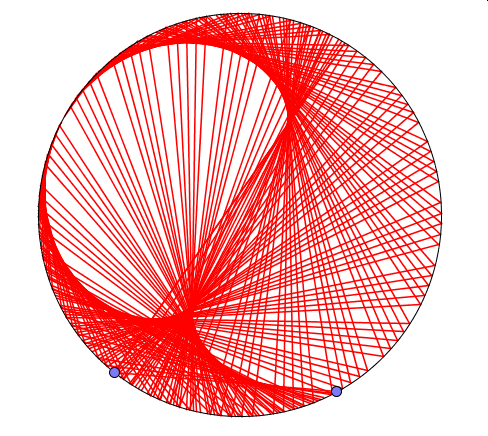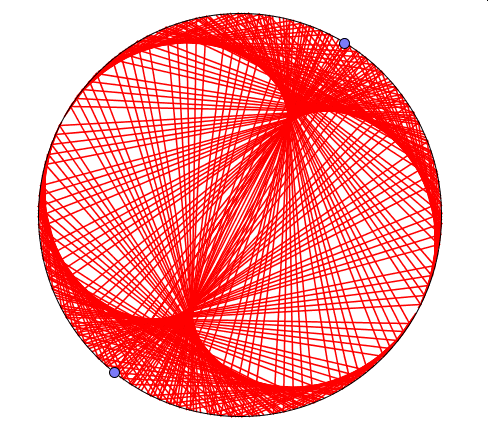
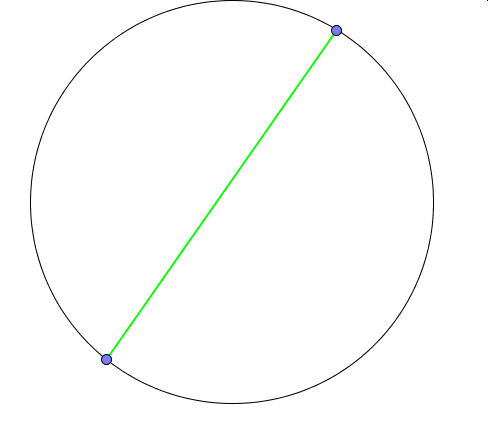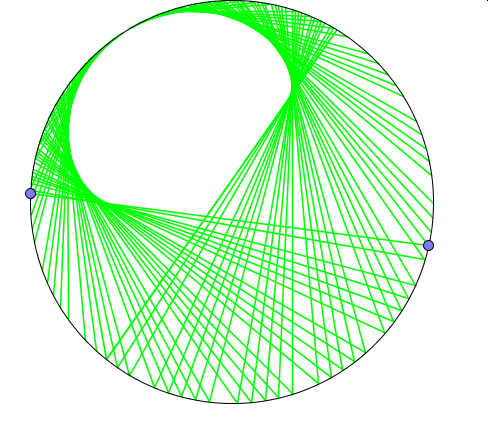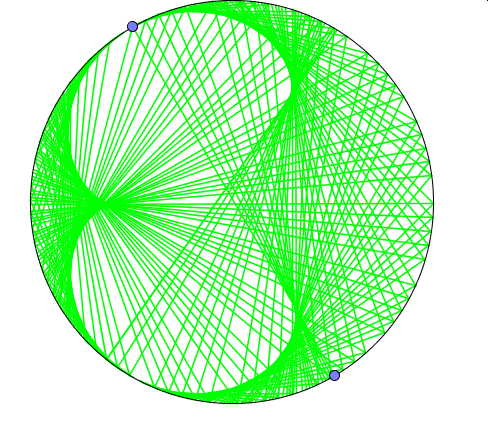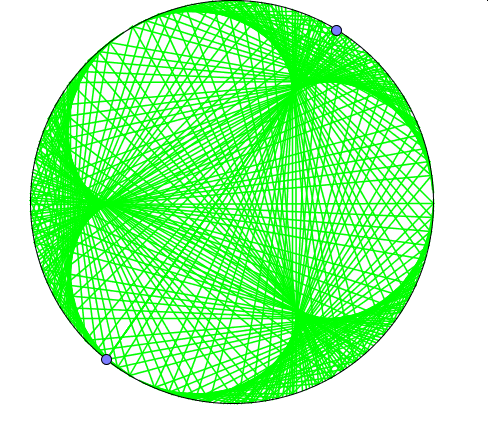
Powyżej widoczne są wyniki trzech doświadczeń.W pierwszym (kolor niebieski) jeden z punktów porusza się dwukrotnie szybciej niż drugi, w kolejnym (kolor czerowy) -trzykrotnie, a w ostatnim(kolor zielony) – czterokrotnie.
Można to sprawdzić obserwując ile razy szybszy punkt wymija wolniejszy.

Jesli chcesz samodzielnie poeksperymentować z wyszywankami, zainstaluj na swoim komputerze GeoGebrę i pobierz plik wyszywanki

Uczniowie klas szkoy podstawowej którzy nie mają możliwości pracować z komputerem mogą sobie wyszyć te piękne krzywe na twardszym kartonie posługując się iglą i nitką. Najpierw na kartonie wykreślamy okrąg o promieniu 8 – 12 cm. Dzielimy go na parzystą liczbę części kreśląc np 36, 48 lub 72 punkty w równych odległościach od siebie. Umówmy sie, że karton ma „prawą” i „lewą” stronę. Prawa to ta, na której zobaczymy wyszywankę, lewa to spodnia część kartonu. Nawlekamy na igłę kolorową nitkę i przewlekamy od strony lewej przez dowolny punkt. Natępnie wbijamy od strony prawej w punkt leżący po przeciwnej stronie wybranego punktu. Otrzymujemy już jeden z odcinków wyszywanki. Jeśli w wyszywance iloraz prędkości poruszanych punktów jest równa np.4, wówczas po przełożeniu igły z nitką pod spodem kartonu przesuwamy się o cztery punkty w umówionym kierunku – np niezgodnie z ruchem wskazówek zegara. Wbijamy tam igłę (od strony lewej) i przechodząc nad prawą częścią kartonu wbijamy igłę w sąsiedni punkt od pierwszego punktu idąc niezgodnie z ruchem wskazówek zegara. Po wbiciu przechodzimy pod spodem do kolejnego punktu niezgodnie z ruchem wskazówek zegara i znowu przechodząc nad prawą stroną kartonu wbijamy igłę w punkt przesunięty o cztery punkty niezgodnie z ruchem wskazówek zegara. Powtarzamy tę czynność stosując tę samą zasadę: jeden punkt przesuwa się o 1 a drugi o 4 pukty niezgodnie z ruchem wskazówek zegara.W końcu wrócimy do pierszego punktu – wyszywanka gotowa.