Stellacja wielościanu polega na przedłużeniu jego ścian do momentu, aż płaszczyzny, w których zawierały się te ściany ograniczą nowy wielościan. Stellację nazywamy też stożkowaniem. Z definicji tej wynika od razu, że nie da sie stellować sześcianu ani czworościanu, gdyż płaszczyzny sześcianu są równoległe, więc nigdy się nie przetną, zaś w czworościanie zamykają one ten sam czworościan.
Ciekawe stellacje posiada dwunastościan foremny. Można z niego otrzymać trzy kolejne stellacje, stellując najpierw dwunastościan, potem jego pierwsza stellację a następnie drugą.
Poniższy gif animowany jest zrzutem ekranu GeoGebry dynamicznej transformacji 12 foremnego w jego pierwszą stellację.
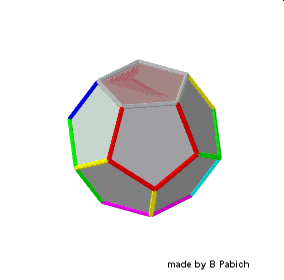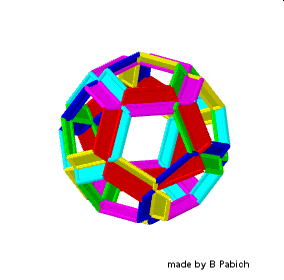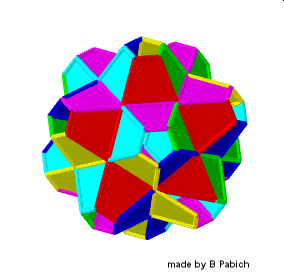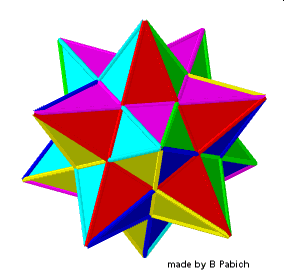
Uzyskany wielościan otrzymał po raz pierwszy matematyk i atronom niemiecki, Johannes Kepler w 1609 roku. Teraz dokonajmy kolejnej, drugiej stellacji 12 foremnego.

Ten wielościan utworzył francuski matematyk Luis Poinsot ok 1850 roku. Kolejną, trzecią stellację uzyskał znowu Johannes Kepler. Możemy podziwiać sposób, w jaki powstaje ona z drugiej stellacji.

Te trzy wielościany pojawiają się w geometrii pod nazwą wielościanów Keplera – Poinsota i należą do grupy czterech wielościanów foremnych wklęsłych, które zwiększają liczbę wielościanów foremnych wraz z bryłami platońskimi do 9.
Czwarty wklęsły wielościan foremny odkryty znowu przez Poinsota nie jest już stellacją dwunastościanu foremnego, lecz stellacją dwudziestościanu foremnego.
Jego ilustracja pojawi się tu w niedługim czasie.
Powtórzmy jescze raz za pomocą jednej animacjią transformację od pierwszej stellacji 12 foremnego do trzeciej:
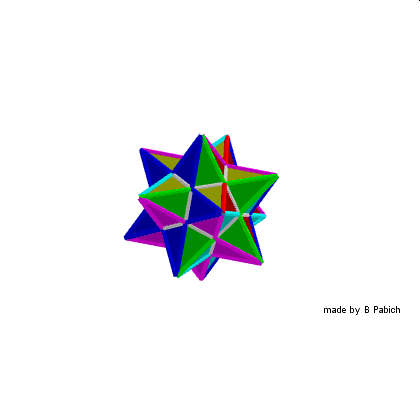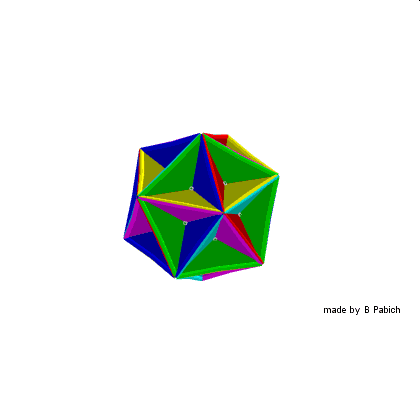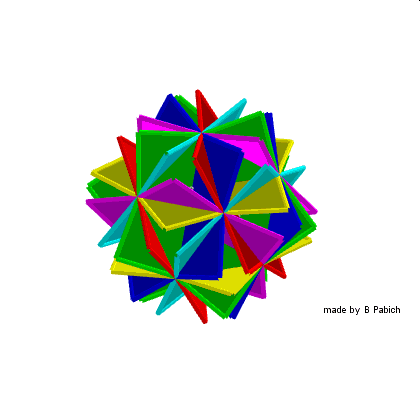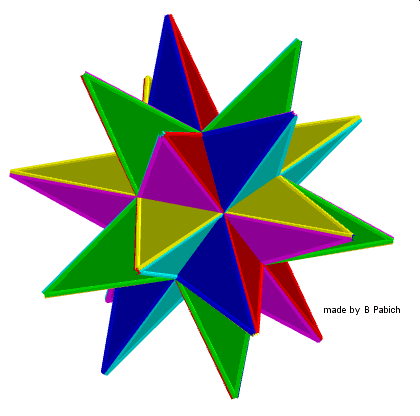
Te cztery wielościany Keplera – Poinsota mają również swoje indywidualne nazwy – kolejno: 1 stelacja 12 foremnego nazywana jest małym dwunastościanem gwiaździstym, 2 stellacja nazywa się dwunastościanem wielkim, zaś 3 stellacja dwunastościanu to dwunastościan gwiaździsty wielki.
Czwarty wielościan a drugi wielościan Poinsota powstaje z dwudziestu trójkątów równobocznych i nosi nazwę dwudziestościanu gwiaździstego wielkiego.