Kto z nauczycieli nie chciałby w trakcie prezentowania na lekcji stereometrii w Szkole Podstawowej lub Liceum znanych wielościanów objętych programem nauczania i ich własności wzbogacić lekcję dynamicznym pokazem siatek tych wielościanów, wydrukować je uczniom i rozdać do domu w celu ich sklejenia. To byłaby idealna lekcja stereometrii. Uczniowie mogliby dotknąć te wielościany, oglądnąć je z różnych stron a posługując się odpowiednią recepturką poszukiwać ich przekroje. Ponadto uczniowie ćwiczyliby swoją wyobraźnię, gdyż oglądanie martwego obrazu nieudolnie kreślonego na tablicy przez wiele cennych minut lekcji jest czystą stratą i pozbawia ich tego co doświadczą w omówiony przed chwilą sposób. Oczywiście sprawa kreślenia odręcznego rzutów wielościanów to niezwykle ważna i cenna umiejętność, ale o tym innym razem.

Dysponując rzutnikiem i aktywną na lekcji GeoGebrą możemy w pełni realizować dynamiczną prezentację wielościanów. Program opcjonalnie oferuje całą gamę ostrosłupów, graniastosłupów oraz wielościanów platońskich. Czasem nawet wystarczy wskazać dwa wierzchołki takiego obiektu i dodatkowo jego wysokość lub inny parametr i wielościan pojawia się na dynamicznym ekranie.

Możemy wówczas zadać uczniom pytania typu: „jakie wielokąty tworzą rzuty wielościanu, który widzisz na ekranie”, „czy to jest rzut perspektywiczny czy równoległy tego wielościanu”, „ile ścian (wierzchołków, krawędzi) ma ten wielościan”, „podejdź do komputera i tak ułóż ten sześcian, by jego rzutem był sześciokąt foremny”.

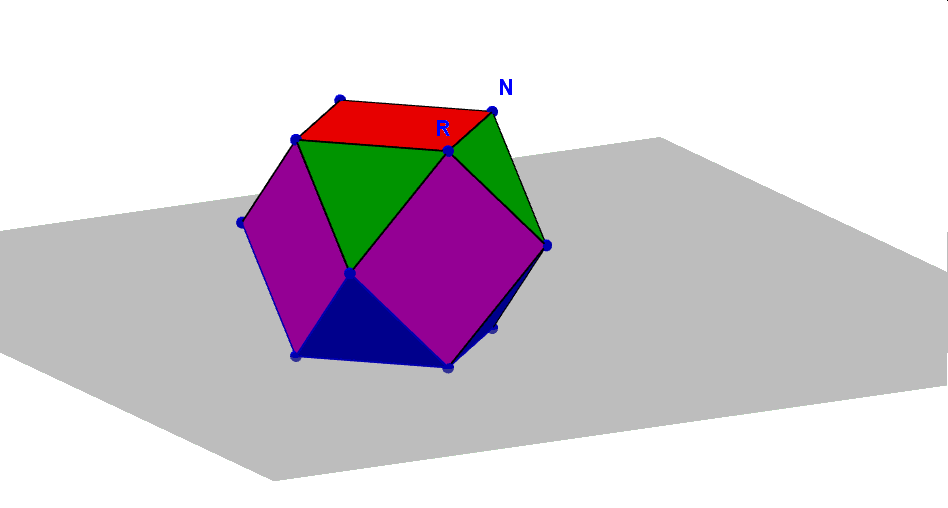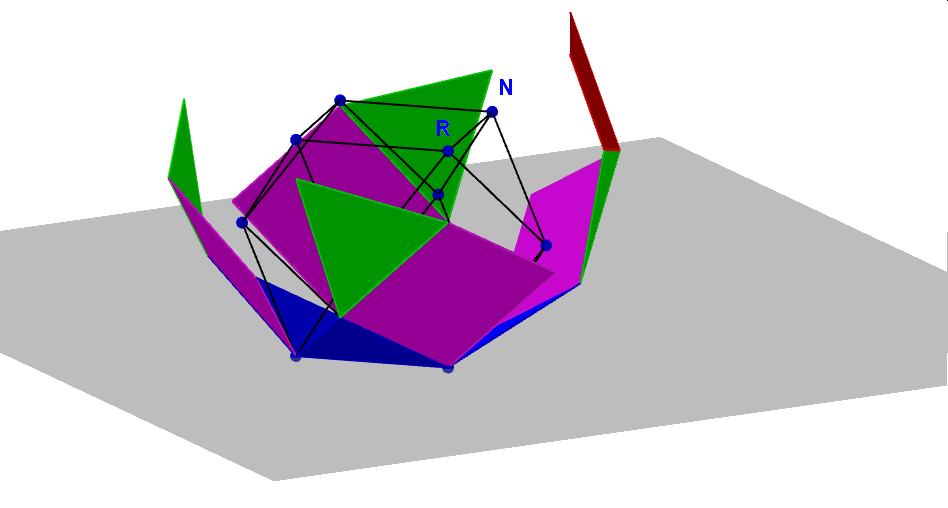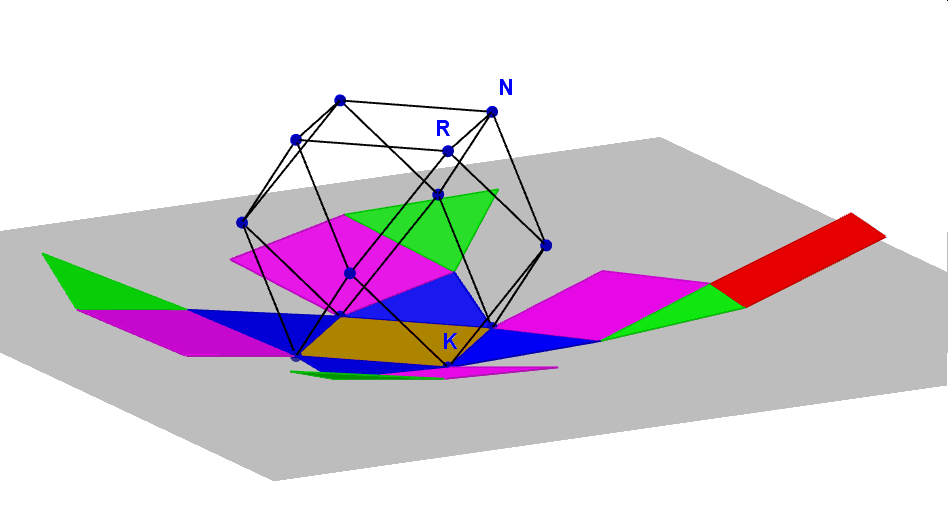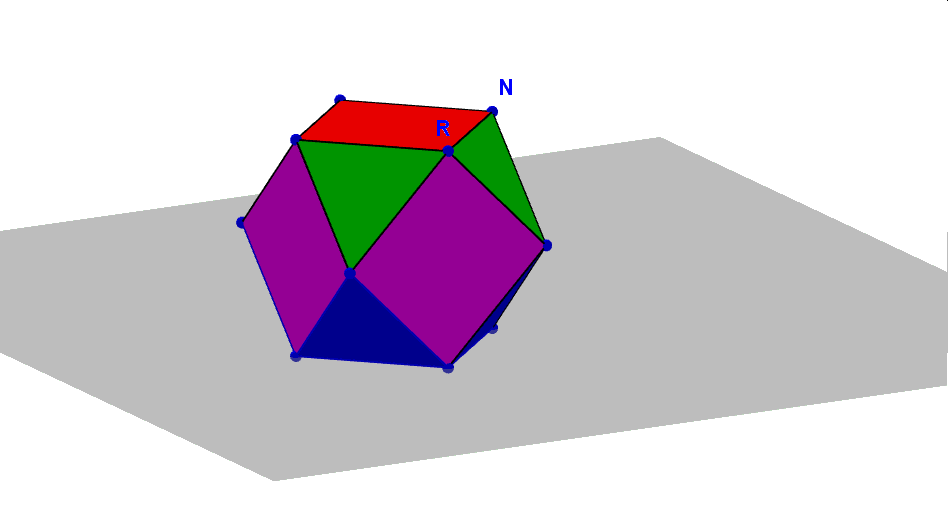
C.d. tego artykułu można przeczytać w egzemplarzu czasopisma „Matematyka – czasopismo dla nauczycieli” nr 1/2019.  Jego efektem końcowym jest siatka sześcioośmiościanu zaprezentowana poniżej w gifie animowanym, wykonana w GeoGebrze. Zauważmy, że kąty dwuścienne w tym wielościanie są wszystkie przystające, gdyż zawarte są zawsze między ścianą kwadratową i trójkątną, zatem łączny obrót wszystkich ścian można dokonać jednym suwakiem. W ten sposób można wykonać dynamiczne siatki wszystkich pozostałych wielościanów Archimedesa, do których właśnie sześcioośmiościan również należy. Ale to zadanie pozostawiam już czytelnikom tej strony i czasopisma „Matematyka dla nauczycieli”.

.