Ukladanki 3D  a objętości brył  (3D puzzles and the volume of solids)

Drukowanie na drukarkach 3D obiektów geometrycznych – obok radości z efektów wydruku – może przynieść jeszcze więcej splendoru z możliwości dydaktycznych w postaci odkrywania ciekawych własności geometrycznych tych obiektów i przystosowania ich do tworzenia interesujących układanek matematycznych.

Przeznaczeniem takich wymyślnych układanek jest na przykład ułożenie z elementów jednego wielościanu innego o tej samej objętości. Nie tylko niosą one za sobą radość z ich układania, ale spostrzegawczemu matematykowi ułatwiają też wykonanie trudnych obliczeń bez skomplikowanych rachunków.

Pierwsza metoda

Na rys. 1 widzimy rozrzucone wielościany. Gdy dokładniej im się przypatrzymy, zauważymy, że są one wszystkie przystające.
Jest ich dokładnie osiem. Intuicja podpowiada, że mogą one mieć związek z ośmiościanem foremnym. Ale intuicji nie wolno dowierzać. Czy można z nich coś ułożyć?

  rys 1

Skoro są jednakowe, to warto je poskładać ze sobą tak, by ich przystające ścianki przylegały do siebie. Zauważmy, że każdy wielościan ma łącznie osiem ścian przystających parami z uwagi na jego symetrię płaszczyznową. W żadnej parze nie powtarzają się przystające ściany.

Odłóżmy cztery z tych wielościanów, a z pozostałych spróbujmy ułożyć jakąś rozsądną figurę, przykładając do siebie przystające ściany. Możemy to uczynić na cztery sposoby, gdyż, jak już wspomnieliśmy, dysponujemy czterema rodzajami ścian. Są to:

• sześciokąt foremny – ryc. 2a,
• sześciokąt różnoboczny – ryc. 2b,
• trójkąt prostokątny duży – ryc. 2c,
• trójkąt prostokątny mały – ryc. 2 d.

rys. 2a, 2b, 2c, 2d

Sześciokąt foremny sugeruje, że z tych ośmiu elementów możemy złożyć jedną z brył Archimedesa, np. czworościan ścięty, ośmiościan ścięty, sześcioośmiościan ścięty, dwudziestościan ścięty lub dwudziestodwunastościan ścięty. Złożenie dwóch brył ścianami sześciokątnymi daje konfigurację, w której dwie ściany są prostopadłe (ryc. 3), a dołożenie do nich jeszcze dwóch o takiej samej konfiguracji pozwala nam dostrzec pół sześcianu (ryc. 4).

rys. 3                                                          rys. 4                                       rys. 5                                         rys. 6

Kolejne cztery identyczne wielościany formują z już ułożonymi pełny sześcian. Prezentuje to poniższy aplet GeoGebry.

Krawędzią tego sześcianu jest najdłuższy bok sześciokąta różnobocznego – ryc. 5.  Inny sposób złożenia otrzymamy dość łatwo – składając ze sobą wielościany ośmiokątami różnobocznymi, najpierw po dwie (ryc. 6), a potem pozostałe dwie. Utworzą one bryłę, która ma dwie prostopadłe płaszczyzny symetrii. Całość prezentuje coś znajomego – ośmiościan ścięty.

Sposób jego tworzenia opisuje poniższy aplet.

Tak więc osiem wielościanów pokazanych na początku artykułu daje albo sześcian, albo dwie przystające bryły Archimedesa – ośmiościany ścięte (ryc. 7 a i b).

rys. 7a i 7b

Ta układanka, w samej naturze prosta, może nam posłużyć do wyznaczenie objętości ośmiościanu ściętego. Odkryliśmy już, że:

V_6scianu = 2 ∙ V_{8 ściętego}

Oznaczmy przez a długość krawędzi sześcianu, z którego powstały dwa ośmiościany ścięte. Ich krawędzie oznaczmy literą x. Poszukajmy relacji między wielkościami a i x. Znajdziemy je, obserwując ścianę, która jest sześciokątem różnobocznym – figura niebieska na ryc. 8.

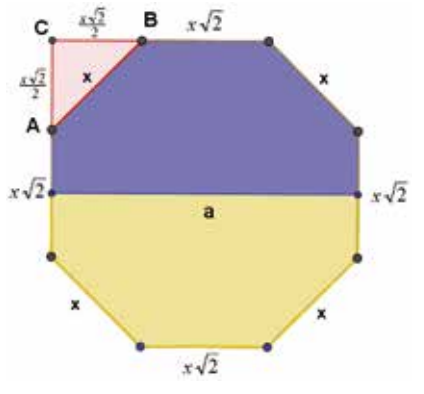 rys. 8

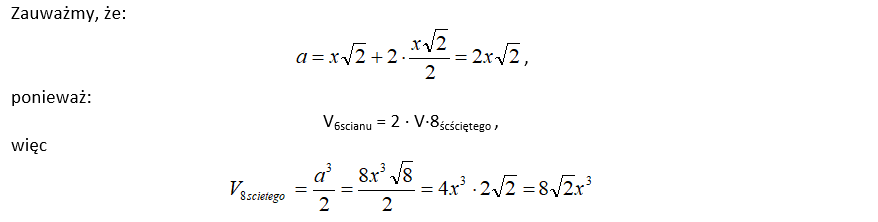
Wyznaczyliśmy objętość ośmiościanu ściętego o krawędzi x.

Druga metoda

To nie jest jedyny sposób wyznaczenia objętości tego wielościanu przez zastąpienie go innymi wielościanami o tej samej objętości.
Wyobraźmy sobie dwa sześciany, każdy rozcięty na dwa kawałki sześciokątnym przekrojem. Rysunek 9 ilustruje te sześciany: biały i czerwony, a rys. 10 cztery elementy po ich rozcięciu.  Składamy je ze sobą tak, by utworzyły one połowę ośmiościanu ściętego.

rys. 9                                                                      rys. 10                                                 rys. 11

Z czterech sześcianów uzyskamy więc w ten sposób jeden ośmiościan ścięty. Rysunek 11 ilustruje połowę tego ośmiościanu. Drugiej, dolnej  jego połowy nie widać. Sposób uzyskania tego ośmiościanu ściętego ilustruje poniższy aplet

Przyjmijmy długość  krawędź każdego z czterech sześcianów jako a. Długość y krawędzi ośmiościanu ściętego jest długością boku sześciokąta stanowiącego przekrój sześcianu. Bok tego sześciokąta łączy środki dwóch sąsiednich boków kwadratu, który jest ścianą sześcianu – ryc. 12.

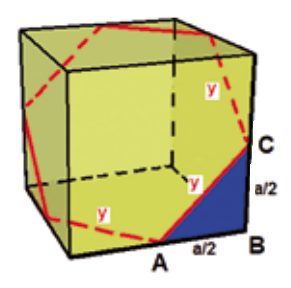rys. 12

Otrzymaliśmy taki sam wynik objętości ośmiościanu ściętego o krawędzi długości y.

Trzecia metoda

Na koniec warto wyznaczyć tę objętość metodami klasycznymi. Objętość ośmiościanu ściętego to różnica objętości ośmiościanu foremnego i objętości sześciu ostrosłupów odciętych w jego narożach w 1/3 każdej krawędzi ośmiościanu (rys. 13).

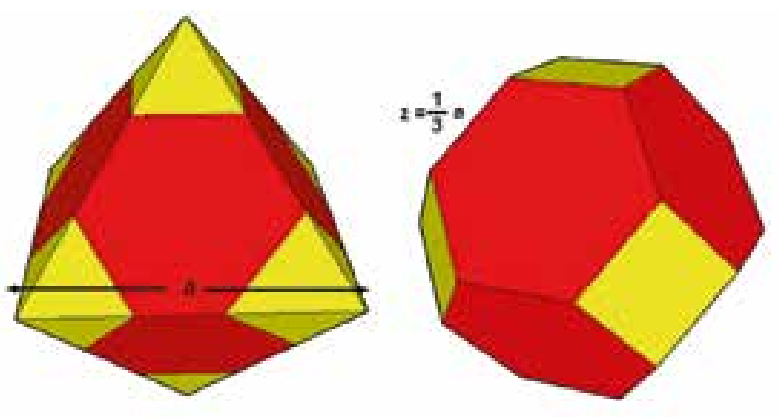
rys. 13

I znowu otrzymaliśmy ten sam wynik. Tak więc mamy przykład zadania geometrycznego rozwiązanego trzema sposobami.
Wyjaśnia to dokładnie poniższy, czwarty aplet GeoGebry.

Czytelnik sam oceni, które z tych rozwiązań przedstawia największą wartość dydaktyczną.

Autor zna sporo układanek, które z jednych wielościanów przez odpowiednie rozcięcie tworzą inne wielościany. Wiele z nich, precyzyjnie wykonane na drukarce 3D, można zakupić na stronie math-comp-educ. pl w dziale „sklep”.

Mają one sporo zalet dydaktycznych, gdyż uczniowie na takich modelach mogą sprawdzać różne własności metryczne tych wielościanów
i pogłębiać swoją wyobraźnię przestrzenną.

 

 

.