Historia III problemu Hilberta (history of third Hilbert’s problem)

W 1900 roku w trakcie Konferencji Matematycznej w Paryżu  słynny niemiecki matematyk David Hilbert postawił na XX wiek 23 problemy które dotychczas były nierozwiązane.
Z elementarnej geometrii wiemy, że każde dwa wielokąty o tym samym polu powierzchni da się tak rozciąć, by z rozciętych kawałków dało się  złożyć drugi wielokąt. David Hilbert nie był pewien, czy da się postąpić podobnie z każdymi dwoma wielościanami o tej samej objętości. Postawił więc na Konferencji ten problem jako problem nr III.

Autor tego artykułu natrafił zupełnie nieświadomie na ten problem umieszczając w sześcianie wielościan odkryty w 1609 roku przez Johannesa Keplera zwany stellą octangulą. Po kilku prostych rachunkach (zachęcam do nich czytelnika) okazało się, że objętość tej stelli stanowi dokładnie połowę objętości sześcianu.

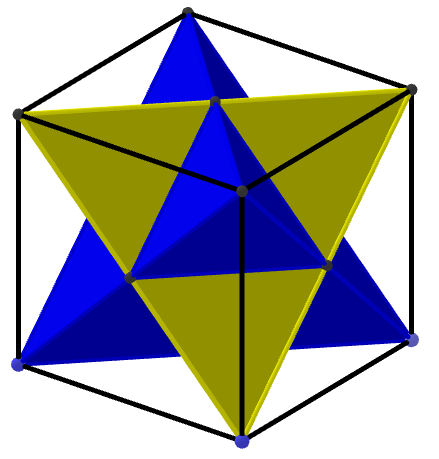
Od razu pojawiło się pytanie, że skoro tak jest, to  stella octangula i jej uzupełnienie do sześcianu mają te same objętości. Próbowałem więc rozciąć osiem części uzupełniających stellę do sześcianu tak, by otrzymać po złożeniu drugą stellę. Jednak bezskutecznie….

Wprawdzie z czterech kawałków udało się złożyć ośmiościan znajdujący się wewnątrz stelli. Poniższy film ilustruje wybór czterech górnych części uzupełniających pomalowanych kolorem zielonym i fioletowym, które w dalszym etapie obracamy tak, by złożyć z nich ośmiościan foremny przystający do tego, na którego bazie powstała stella octangula. Ośmiościan ten jest częścią wspólną dwóch czworościanów foremnych umieszczonych w sześcianie w taki sposób, by ich wierzchołki były równocześnie jego  wierzchołkami.

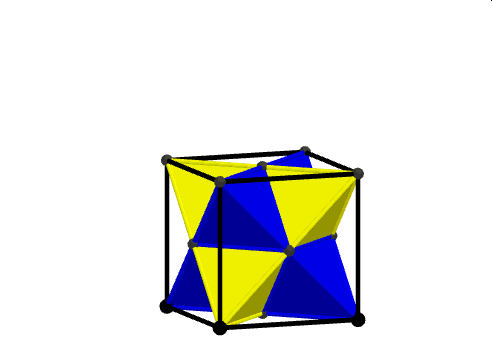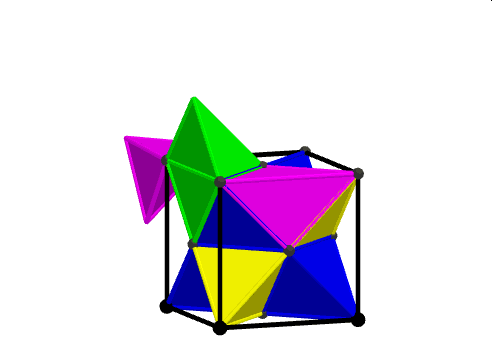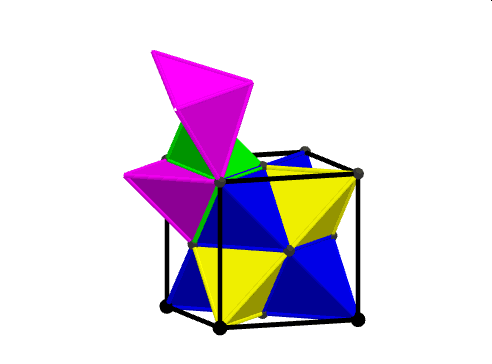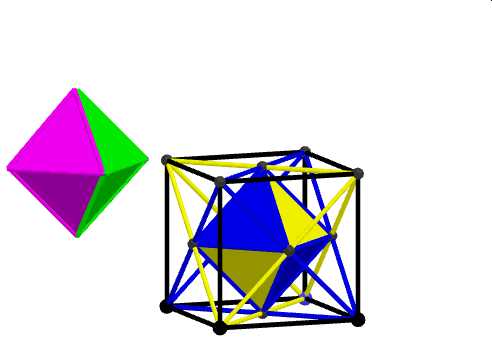
Natomiast z pozostałych ośmiu części uzupełniających stellę do sześcianu nie dało się złożyć jej ośmiu ramion.

 

Krótko mówiąc, żadna z tych ośmiu przystających części nie daje się rozciąć na jedno z przystających ośmiu ramion gwiazdy.   Tak właśnie poznałem praktycznie problem Hilberta. Być może on sam podobnie go odkrył.
Czy zatem moje próby rozkrojenia elementów o tej samej objętości były nieudolne, czy faktycznie tego się nie da rozciąć? Takie samo pytanie postawił sobie Dawid Hilbert. Jaki jest powód niemożliwości rozcięcia wielościanów  Dziś sformułujemy ten problem nieco inaczej: kiedy dwa wielościany o tej samej objętości są równoważne przez rozcięcie?
Zanim odpowiemy na to pytanie, poznajmy takie dwa wielościany o tych samych objętościach z których jeden  da się rozciąć tak, by z rozciętych elementów zbudować drugi.

Czworościan Hilla (Hills tetrahedron)

Wiemy, że dla każdego graniastosłupa o danej podstawie i objętości można skonstruować ostrosłup o tej samej objętości i podstawie. Wystarczy by jego wysokość była trzykrotnie większa od wysokości graniastosłupa.

Ale jak skonstruować ten ostrosłup tak, by dało się graniastosłup rozciąć na kilka elementów z których da się złożyć ten ostrosłup. Zadanie okazuje się nie takie proste.

Po raz pierwszy dokonał tego angielski matematyk Micaiah John Muleer Hill (1885-1929) – który skonstruował graniastosłup o podstawie będącej równoramiennym trójkątem  prostokątnym i odpowiednio dobranej wysokości.  Poniższy film prezentuje sposób rozcięcia a następnie takie rozmieszczenie rozciętych elementów, z których da się zbudować ostrosłup – czworościan o tej samej podstawie i objętości co graniastosłup:

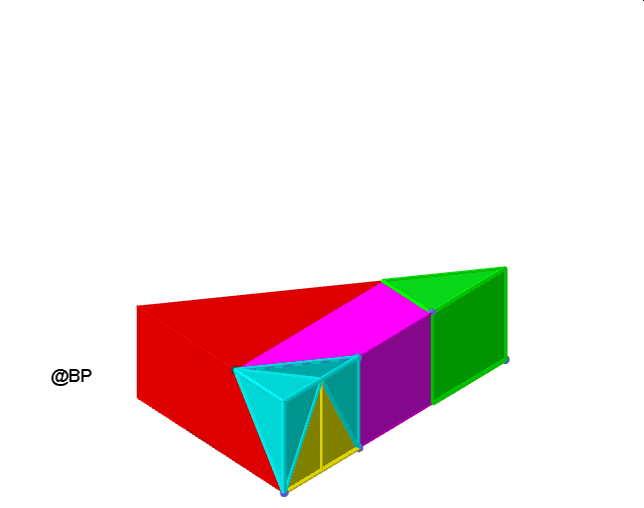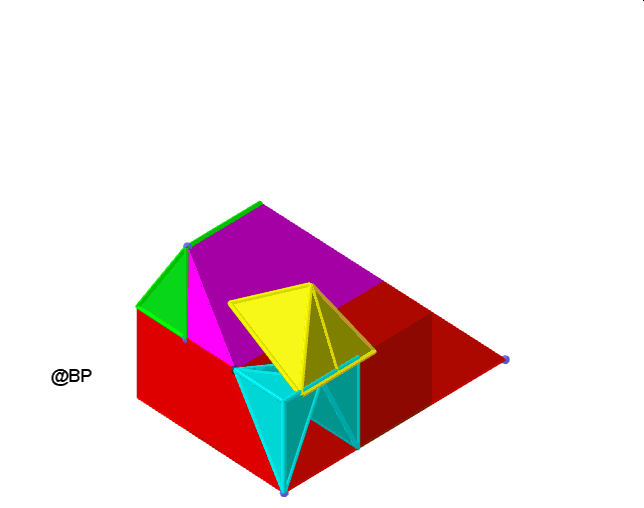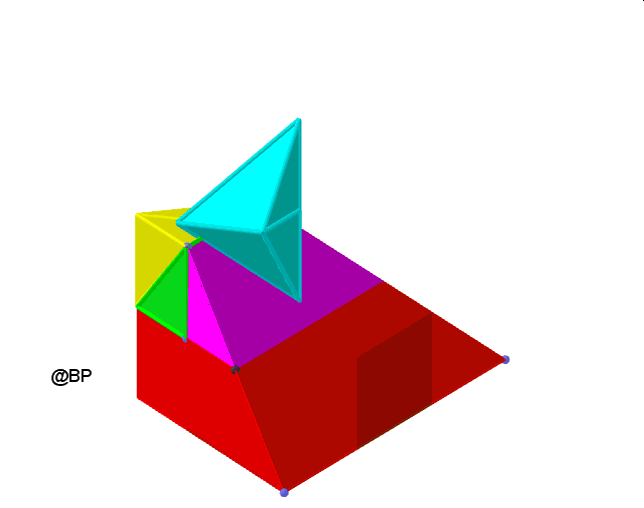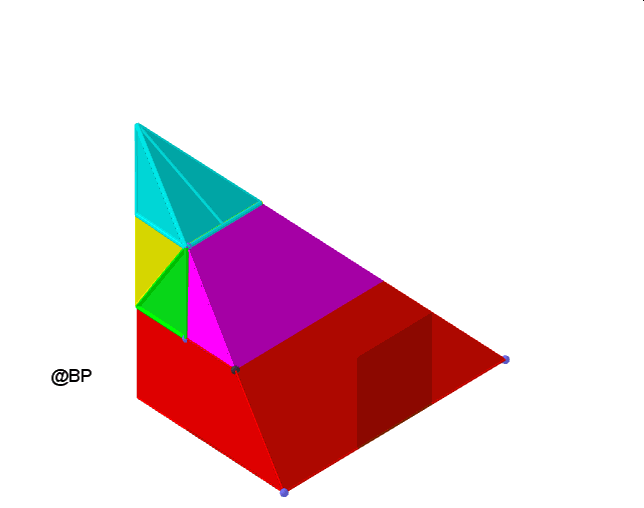
Może czytelnik  obserwując tę animację spróbuje skonstruować z kartonu graniastosłup rozłożony na 7 elementów, z których można ułożyć ostrosłup? Ostrosłup ma z oczywistych powodów wysokość trzykrotnie większą od wysokości graniastosłupa. Zbadajmy dokładniej oba wielościany.

Współczynnik Dehna

Niecały rok po ogłoszeniu przez Hilberta jego III problemu pojawiło się rozwiązanie, którego autorem był doktorant profesora Hilberta – Niemiec o nazwisku Max Dehn. Wprowadził on dla wielościanu  pojęcie współczynnika, którego wartość wyznaczymy dla omówionych  powyżej graniastosłupa i  ostrosłupa.