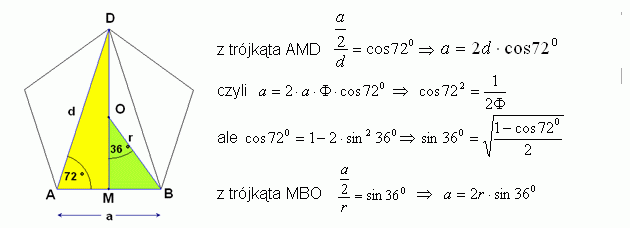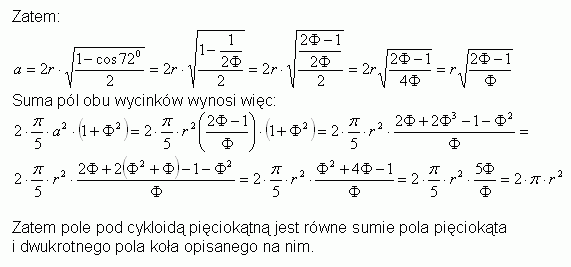
Jazda rowerem, który ma kwadratowe, pięciokątne lub sześciokątne „koła” na pewno nie należy do wygodnych, a jazdę na trójkątnych „kołach” naprawdę trudno sobie wyobrazić.  Matematyka jednak interesują takie rowery. Interesujący jest bowiem ślad jaki wykreśli w trakcie jazdy rowerem jeden z wierzchołków wielokąta, który jest „kołem” tego niezwykłego wehikułu.
Krzywe, które wykreśla  wierzchołek obracajego się po prostej wielokąta nazwijmy  „cykloidami wielokątnymi” gdyż przypominają toczenie sie koła po prostej.
Najprostszą cykloidę zakreśla trójkąt równoboczny. Nazwijmy ją trójkątną. Jak widać poniżej, na cykloidę trójkątną składają się dwa przystające łuki o kątach środkowych o mierze 120°.

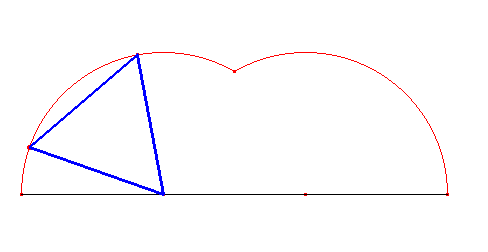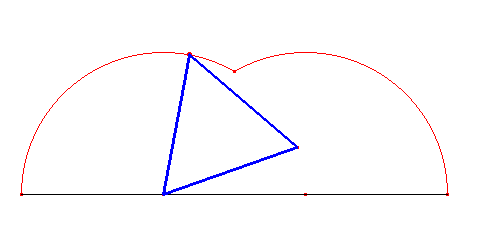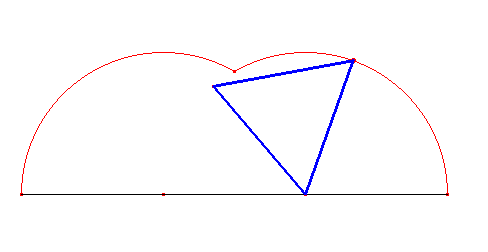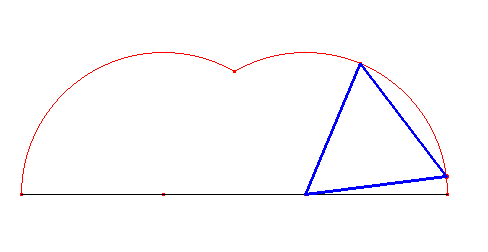
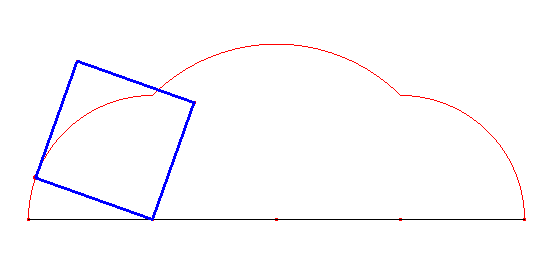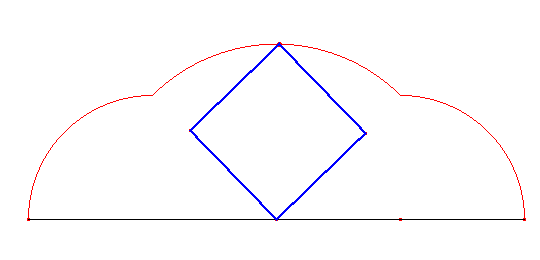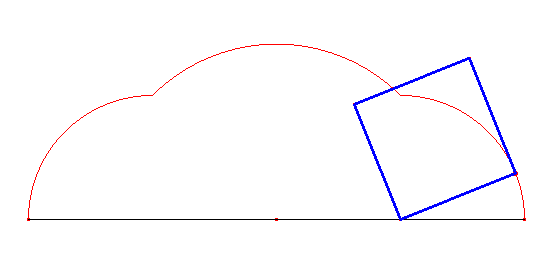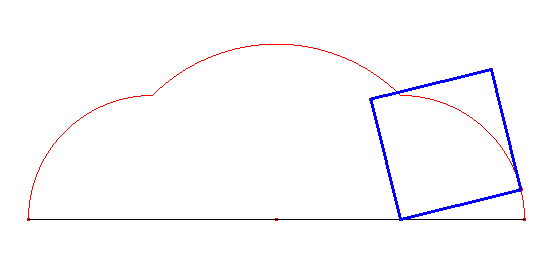
Cykloida kwadratowa powstaje z obracania kwadratu i składa się z trzech łuków, z których dwa są przystające, a trzeci jest nieco większy od nich.

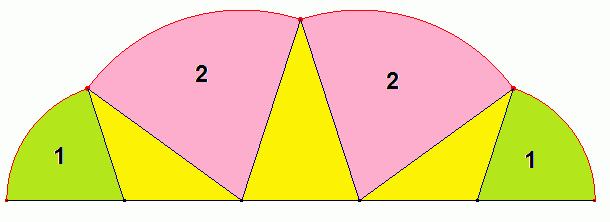
Wierzhołek obracającego się pięciokąta foremnego zakreśla cykloidę pięciokątną o czterech, parami przystajacych  łukach.

Obserwując   te trzy przypadki nasuwa sie hipoteza:

ilość łuków jakie zakreśla obracający się  n-kątny wielokąt foremny wynosi n-1.

Dowód tego faktu jst  prosty – przecież pełnego obrotu dokonujemy w wyniku obracania go wokół n-1 jego wierzchołków.

Warto pokusić się na wyznaczenie pola ograniczonego wielokątnymi cykloidami i prostą, po jakiej się obracają wielokąty. Przypatrzmy się na ich obszary:

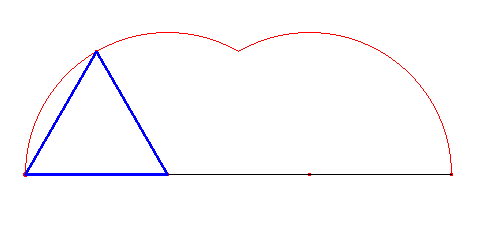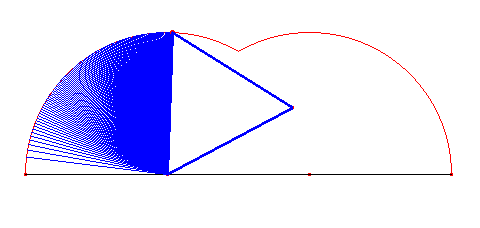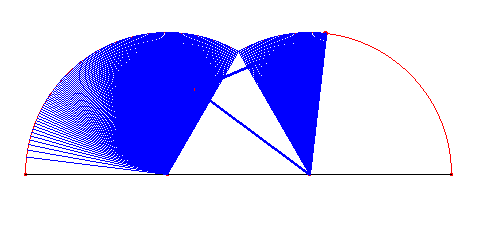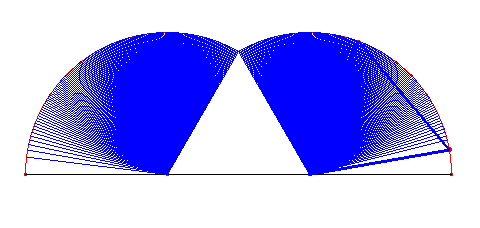
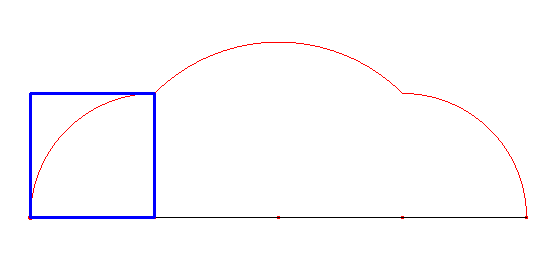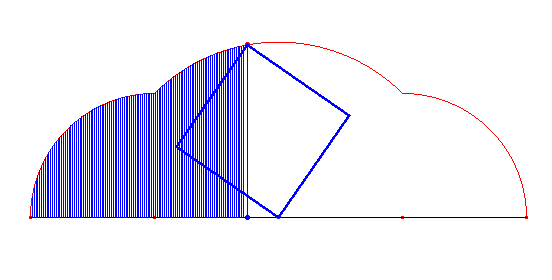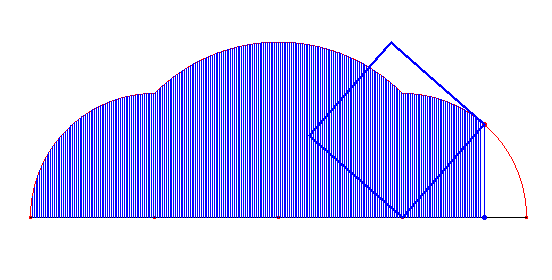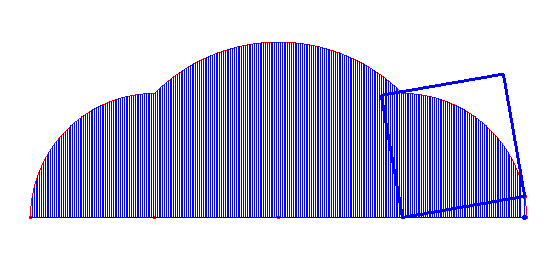
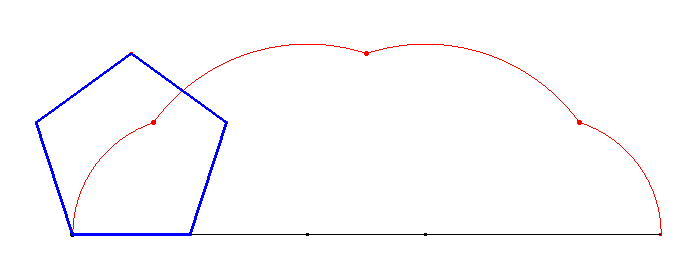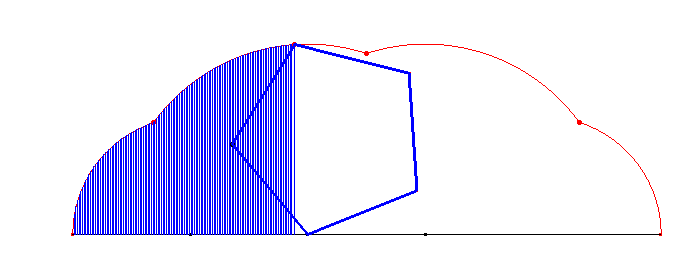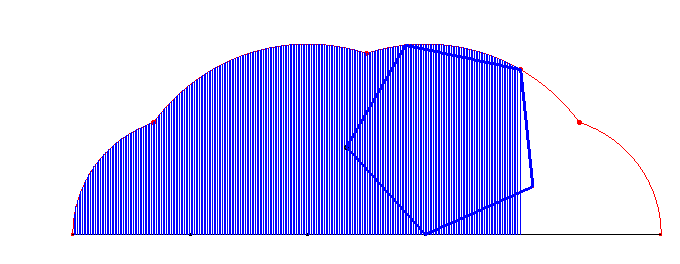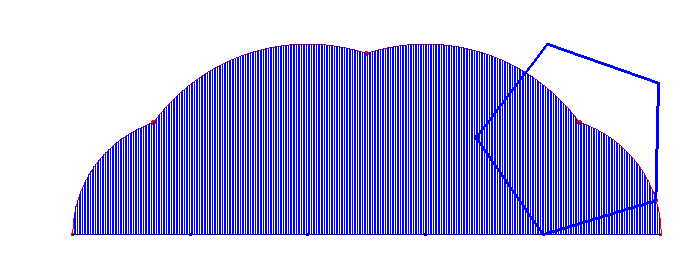
Dla cykloidy trójkątnej:

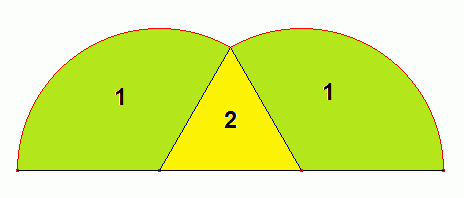
Dla cykloidy kwadratowej:

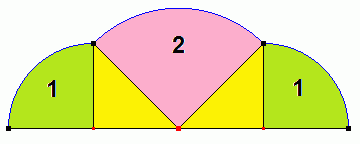
Dl cykloidy pięciokątnej: