Wielościanem nazywamy figurę geometryczną będącą sumą skończonej ilości czworościanów, przy czym dowolne dwa punkty tej figury można połączyć łamaną leżącą w tej figurze. Czworościany na które można rozłożyć wielościan stanowią jego triangulację. Każdy wielościan można poddać triangulacji. Podobnie jest na płaszczyźnie, gdzie każdy wielokąt jest sumą skończonej ilości trójkątów, które stanowią jego triangulację.
WIELOŚCIANY JEDNORODNE (Uniform polyhedra)
Najszerszą grupą wielościanów są wielościany jednorodne. Są to takie wielościany w których wszystkie ściany są wielokątami foremnymi (niekoniecznie tego samego rodzaju) i niekoniecznie wypukłymi) a wierzchołki są przystające. Dzielą się na wielościany jednorodne wypukłe i wklęsłe. Do wypukłych zaliczamy 5 wielościanów platońskich i 13 wielościanów archimedesowskich. Do wklęsłych wielościanów jednorodnych należy grupa 54 wielościanów wklęslych, które są przedstawione poniżej.
Wielościany platońskie (Platonic polyhedra)
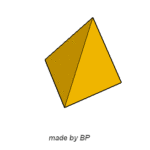
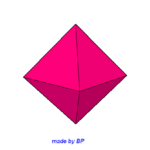
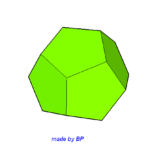
Wielościany, których wszystkie ściany są wielokątami foremnymi przystającymi do siebie a naroża są foremnymi kątami bryłowymi (w jęz. ang. regular polyhedra). Istnieje 5 wielościanów foremnych które opisał już Platon – stąd ich nazwa wielościany platońskie: czworościan, sześcian, ośmiościan, dwunastościan, dwudziestościan. Klikajmy w każdy z nich by zobaczyć je w ruchu.
czworościan sześcian ośmiościan dwunastościan dwudziestościan
Przyglądając sie wielościanom platońskim można dostrzec, że gdyby połączyć środki ścian sześcianu odcinkami, to otrzymalibyśmy krawędzie ośmiościanu foremnego i na odwrót: odcinki łącące środki ścian ośmiościanu foremnego mogą być krawędziami pewnego sześcianu. Podobnie rzecz się ma z dwunastościanem i dwudziestościanem.
Dwa wielościany w których środki ścian jednego są wierzchołkami drugiego i na odwrót nazywamy wielościanami dualnymi. Tak więc sześcian jest dualny z ośmiościanem, a dwunastościan z dwudziestościanem. A z czym jst dwoisty czworościan foremny?
Zwróćmy też uwagę, że w wielościanach dualnych liczba krawędzi jest taka sama. Obliczmy liczbę krawędzi par: sześcianu i ośmiościanu oraz dwunastościanu i dwudziestościanu. Wszystko się zgadza, prawda?
Dla tych, którzy chcą dokładniej zgłębić tajemnice czworościanu foremnego zapraszamy do obejrzenia filmu „Czworościan” który jest dostępny w dziale „filmy”.
Wielościany archimedesowskie (Archimedian polyhedra)
zwane też półforemnymi to wielościany, których ściany są foremne ale niekoniecznie tego samego rodzaju zaś naroża są wszystkie przystające. Powstają z wielościanów foremnych przez obcięcie płaszczyzną ich naroży. Wyjątek stanowią dwa wielościany sześcian przycięty i dwunastościan przycięty które powstają w inny sposób, o czym będzie mowa nieco później.
W narożach wielościanów archimedesowskich powstają wielokąty foremne, nadając wielościanowi charakter jednorodności. Ilość krawędzi w ścianie wielokąta ściętego jest dwukrotnie większa, niż ilość krawędzi ściany wielościanu bazowego, z którego powstał.
Jeśli płaszczyzny przecięć stykają się ze sobą w środku każdej krawędzi, wówczas ściany nowo utworzonego wielościanu są tego samego rodzaju, co ściany wielościanu bazowego. Gdy przykładowo odetniemy naroża sześcianu do połowy jego krawędzi, to ścięcia będą trójkątami równobocznymi, ale pozostałe ściany nadal będą kwadratami. Uzyskamy w ten sposób sześcioośmiościościan. Wielościany archimedesowskie można podzielić według klas ich symetrii: czworościennej. sześcienno-ośmiościennej i dwunasto-dwudziestościennej. Można zauważyć, że nazewnictwo i pochodzenie tych wielościanów w klasie symetrii sześcienno-ośmiościennej i dwunasto-dwudziestościennej jest bardzo podobne. Poznajmy je kolejno:
Wielościany Archimedesa symetrii czworościennej – jest tylko jeden taki wielościan: czworościan ścięty.
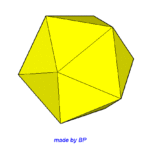
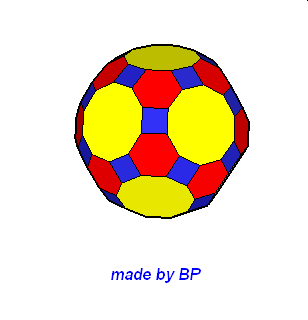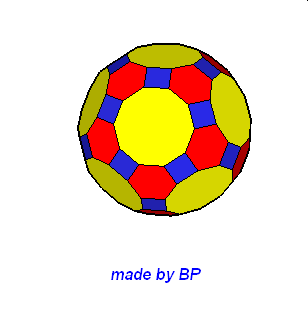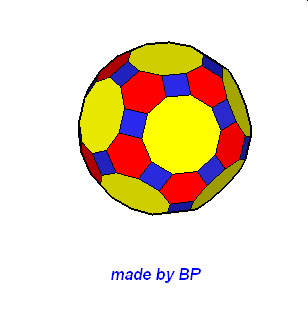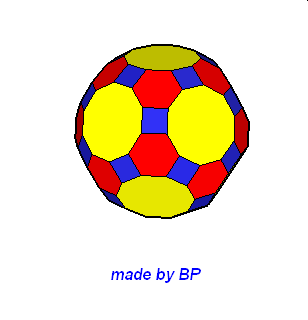
Wielościany Archimedesa symetrii sześcienno-ośmiościennej – jest ich sześć: sześcian ścięty, ośmiościan ścięty, sześcioośmiościan, sześcioośmiościan rombowy, sześcioośmiościan rombowy wielki, sześcian przycięty:
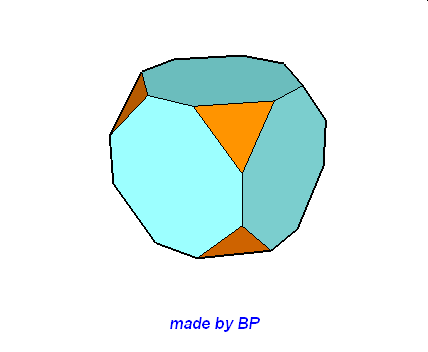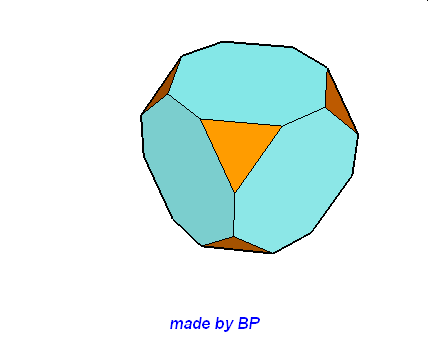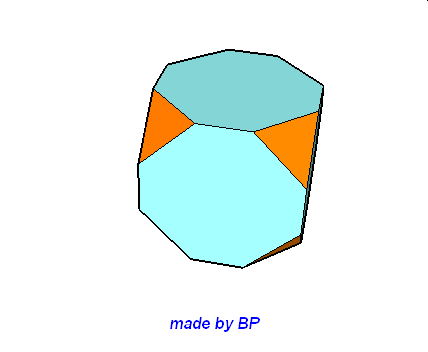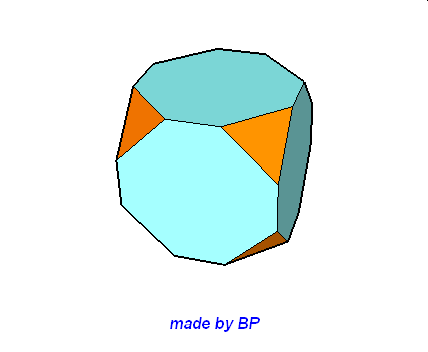
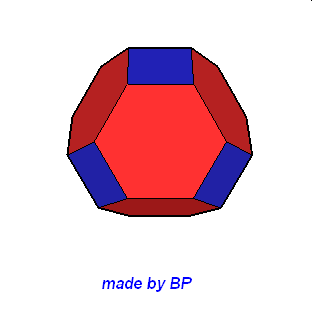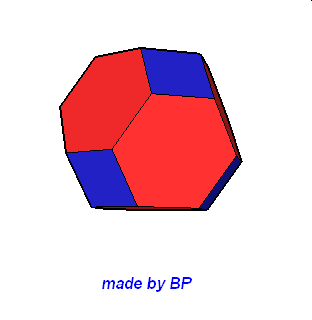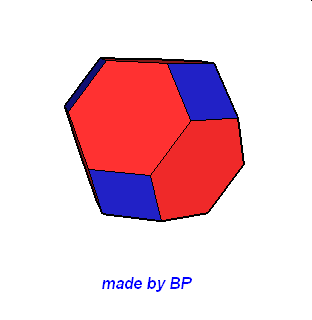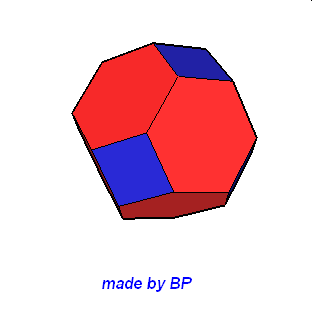
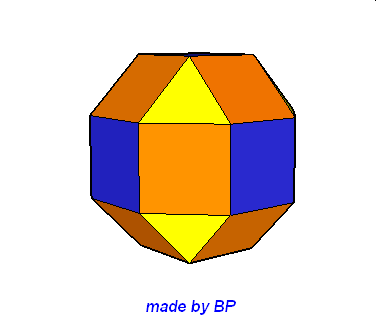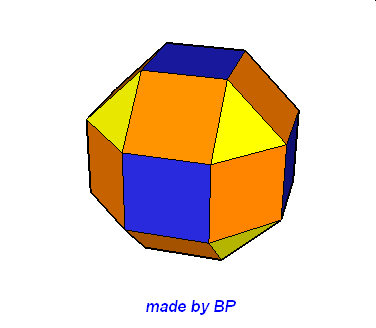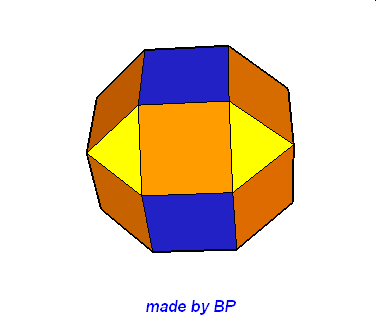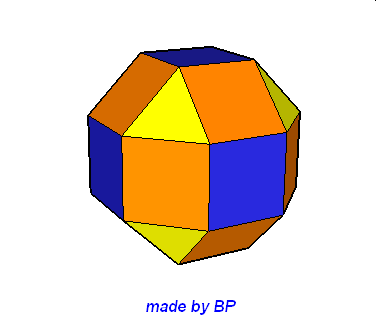
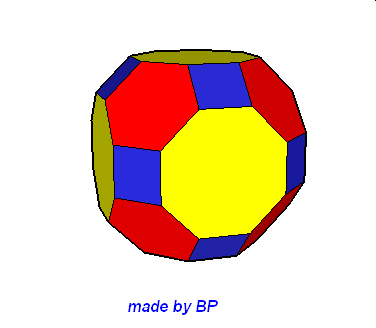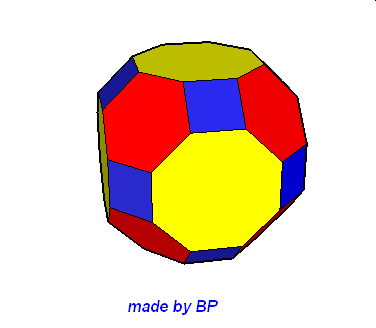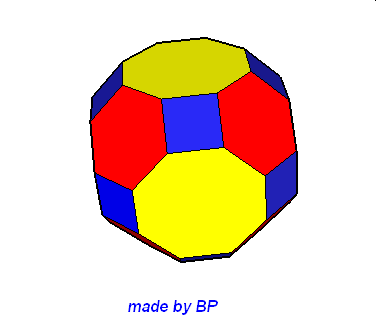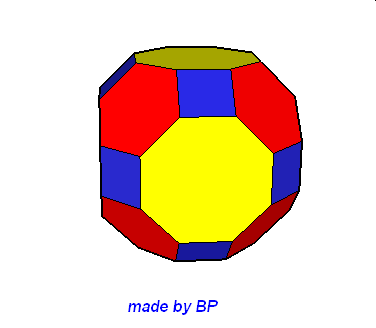
Wielościany Archimedesa symetrii dwunasto-dwudziestościennej – jest ich również sześć: dwunastościan ścięty, dwudziestoscian ścięty, dwunastodwudziestościan, dwunastodwudziestościan rombowy, dwunastodwudziestościan rombowy wielki i dwunastościan przycięty.
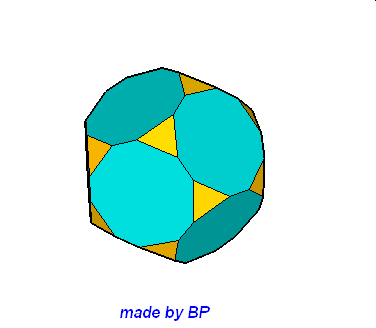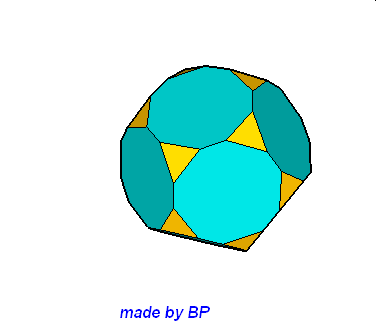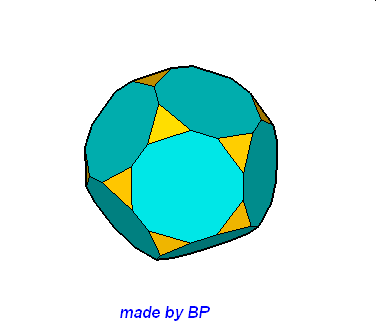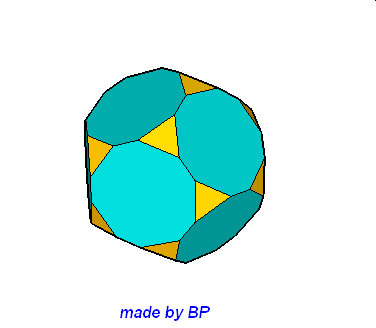
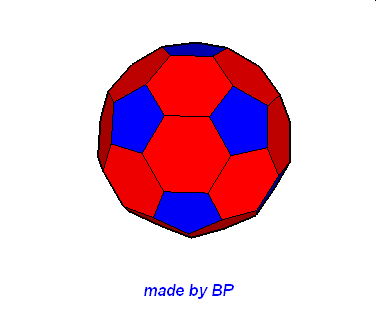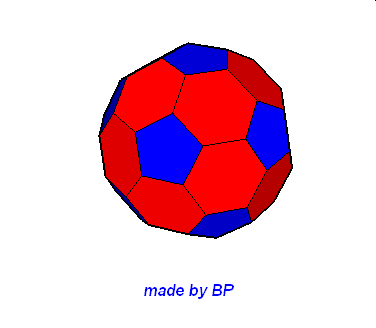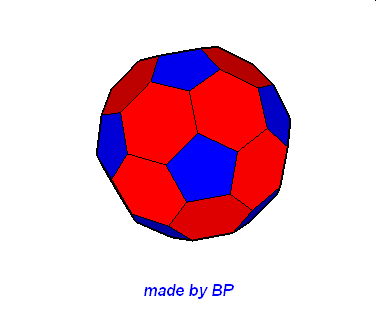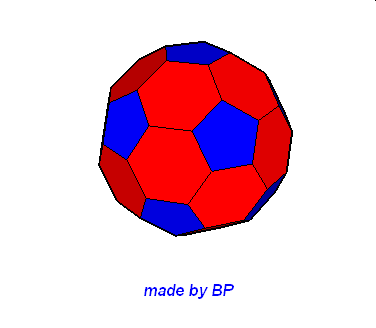
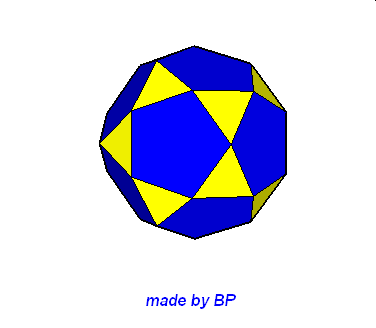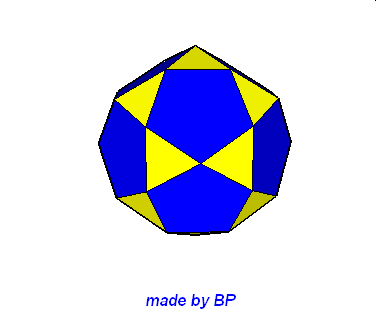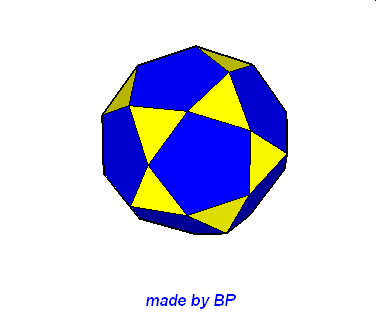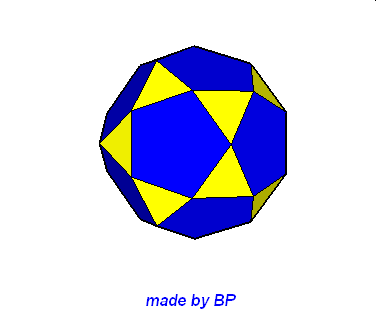
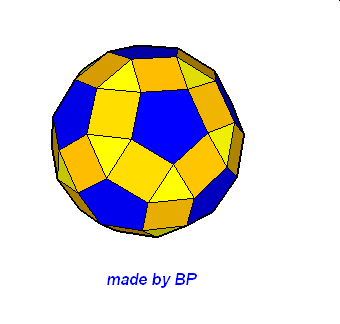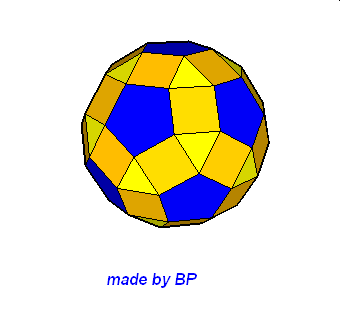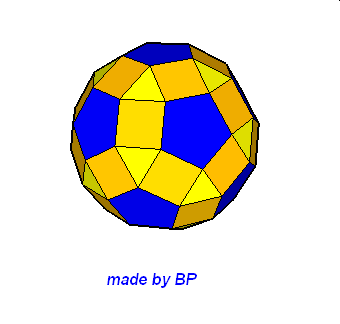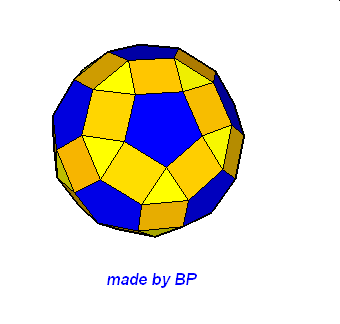

Jeśli ktoś zapragnąłby wyznaczyć objętość wybranej bryły archimedesowskiej to zadanie może okazać się dość trudne. Ale czasami można taką bryłę zamienić na całkiem inną ale równoważną jej objętościowo, której objętość da się dość szybko wyznaczyć. Poniżej mamy przykład zamiany ośmiościanu ściętego w graniastosłup sześciokątny, którego objętość możemy wyznaczyć metodami szkolnymi.
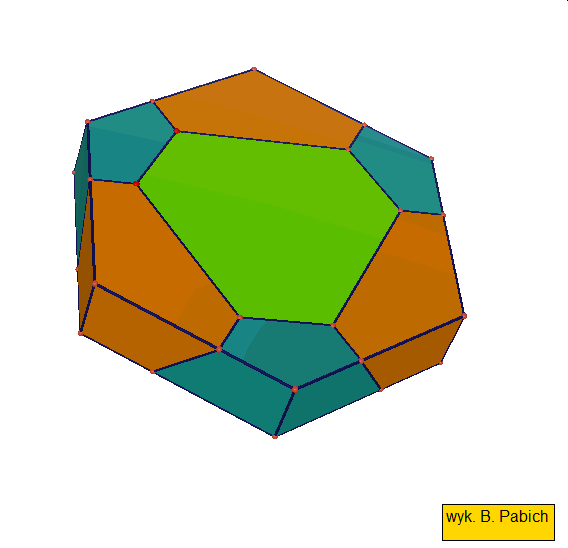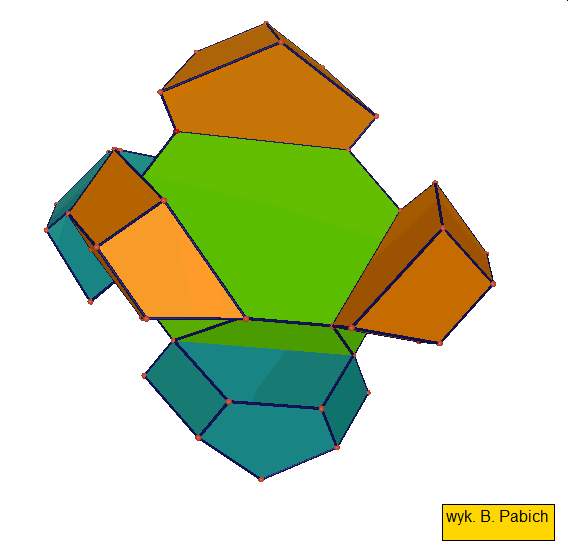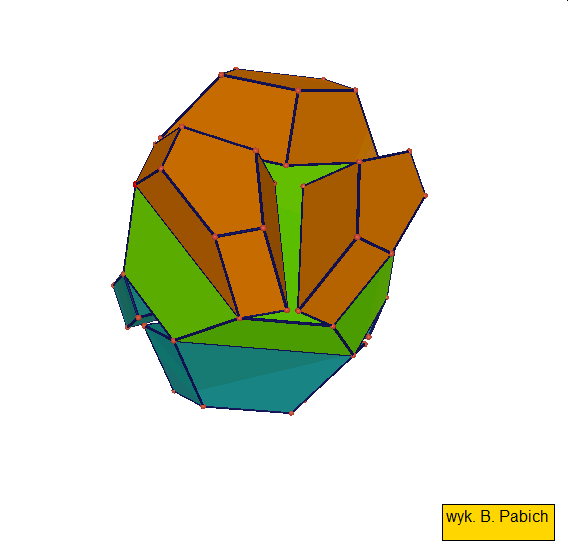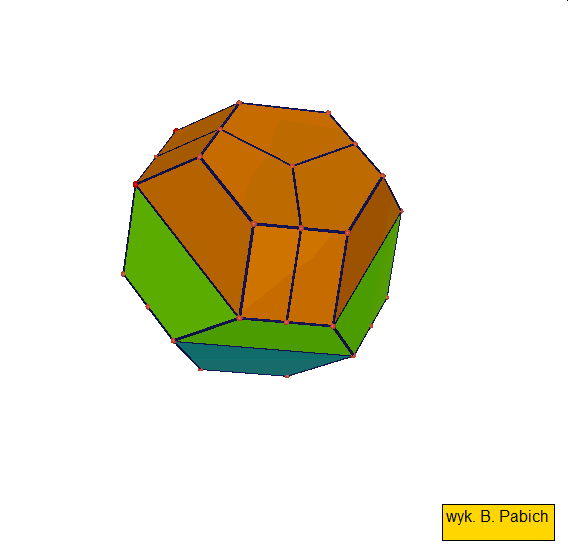
Zwróćmy uwagę na dwa ostatnie wielościany archimedesowskie każdej z tych dwóch grup: sześcian przycięty
i dwunastościan przycięty. Gdy Archimedes je sklejał z papirusu, złożył ze sobą kwadraty z trójkątami oraz pięciokąty z trójkątami i uzyskał te wielościany. Czyli stworzył ich siatki. Natomiast w dobie komputerów
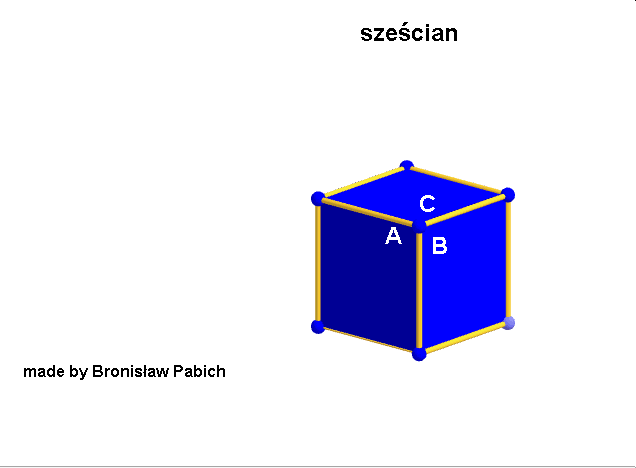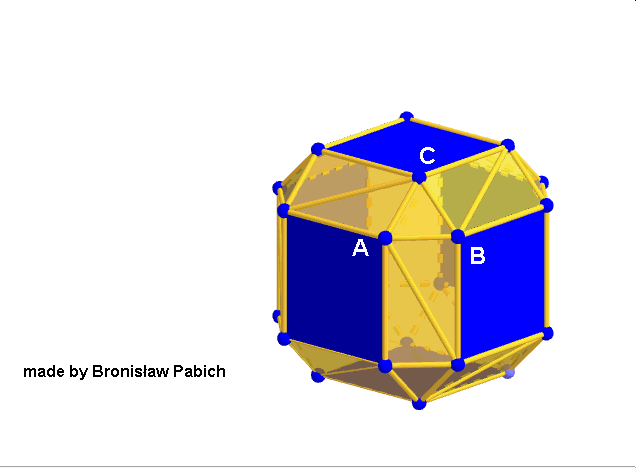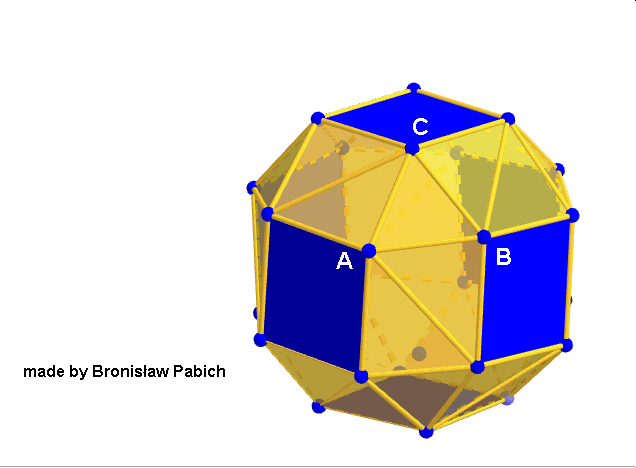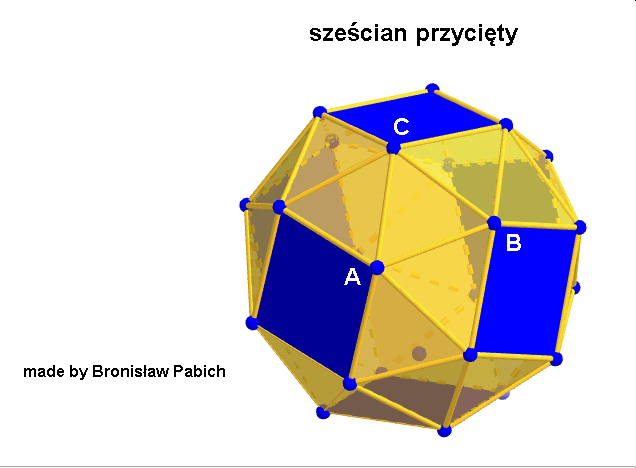
i programów geometrii dynamicznej chciałoby się je stworzyć w przestrzeni za pomocą cyrkla i linijki tak jak inne wielościany Archimedesa. Niestety programy mogą stworzyć te wielościany tylko przez podanie współrzędnych ich wierzchołków, które trzeba wyliczyć w skomplikowany sposób algebraicznie. Rzecz polega na tym, że sześcian przycięty (z ang. snub cube) powstaje z sześcianu przez oddalenie jego ścian na pewną odległość i doprowadzenie go do sześcioośmiościanu rombowego a następnie skręcenie tych kwadratowych ścian o pewien kąt tak, by podzieliły się na trójkąty równoboczne. Poniższa animacja pokazuje ten sposób. Podobnie powstaje dwunastościan przycięty (z ang. snub dodecahedron).
Sześcian przycięty (snub cube)
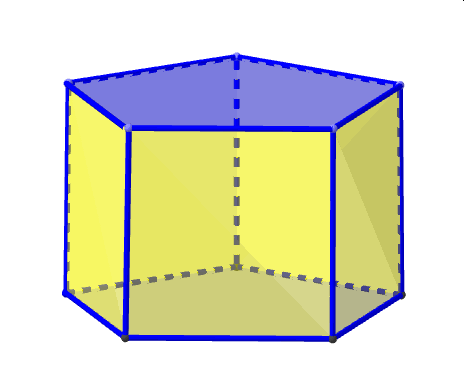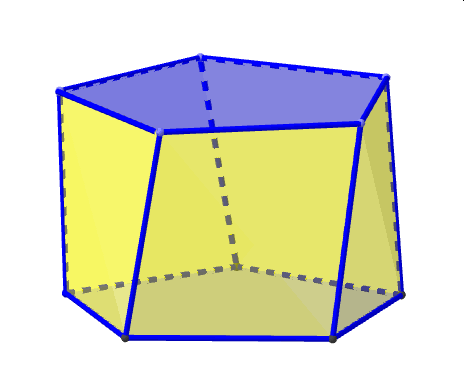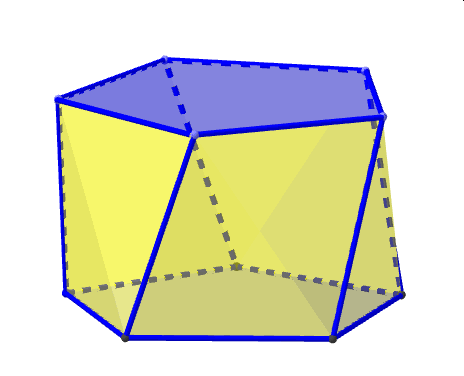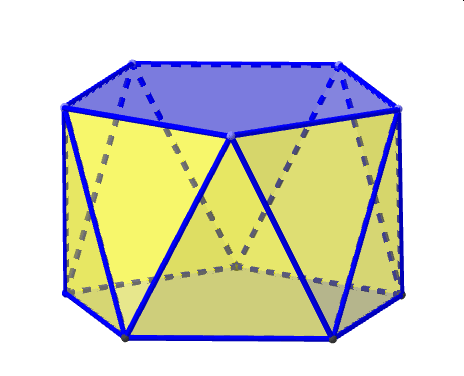
Rodzinę wielościanów archimedesowskich zamyka nieskończona rodzina graniastosłupów o ścianach kwadratowych i antygraniastosłupów powstałych z tych graniastosłupów przez skręcenie jednej z podstaw względem drugiej o kąt
o mierze będącej połową kąta o wierzchołku w środku tej sci any i ramionach łączących ten środek z dwoma kolejnymi wierzchołkami podstawy. Ilustruje to poniższa animacja dla graniastosłupa pięciokątnego. Tutaj obrót nastąpił o kąt o mierze 36°.
PIĘCIOKĄTNY ANTYGRANIASTOSŁUP ( pentagonal antyprism)
WIELOŚCIANY CATALANA (Catalan polyhedra as dual to Archimedian polyhedra)
Dla każdego wielościanu archimedesowskiego istnieje wielościan dualny do niego. Wielościany te opisał w 1865 roku francuski matematyk (niektórzy uważają go za Belga). Poniżej prezentujemy zestaw tych wielościanów w takiej kolejności, w jakiej występowały ich odpowiedniki w zbiorze brył Archimedesa.

czworościan potrójny





ośmioscian sześciościan dwunastościan dwudziestoczworościan ośmiościan
potrójny poczwórny rombowy trapezowy szóstkowy
 .
.



dwudziestoczworościan dwudziestościan dwunastościan trzydziestościan sześćdziestoscian
piątkowy ↨ potrójny piątkowy rombowy trapezowy


dwudziestoscian sześćdziestościan
szóstkowy piątkowy
Spośród wieloscianów Catalana na szczególną uwagę zasługują dwa wielościany: dwunastościan rombowy
i trzydziestościan rombowy. Pierwszy z nich odkrył ok 1609 r. Johannes Kepler, którego nazwisko będzie się jeszcze wielokrotnie przewijałao na tym portalu. Tym wielościanom będzie poświęcona specjalna strona.
WIELOŚCIANY JEDNORODNE WKLĘSŁE
Wielościany jednorodne wklęsłe należą również do klasy wielościanów, które powstają z brył Platona i Archimedesa przez takie ich przekroje, które sś wielokątami foremnymi, niekoniecznie wypukłymi. Jest ich łącznie 54.
Też występują w trzech grupach symetrii: czworościennej, ośmiościenno-sześciennej i dwunasto-dwudziestościennej.
Konstruowanie tych wielościanów w SketchUp jest bardzo trudne i wymaga dobrej znajomości samych wielościanów, przekształceń geometrycznych i elementów geometrii wykreślnej. Zachęcam oglądających tę stronę do sporządzenia kilku z nich. Uczniowie XX LO w Krakowie w ciągu kilku lat (dwie grupy uczniów) wykonali pod moim kierunkiem w programie GeoGebra modele kartonowe wszystkich tych wielościanów. Ich wystawa ucieszyła oczy matematyków uczestniczących w Zjeżdzie z okazji 100-lecia utworzenia Polskiego Towarzystwa Matematycznego w Krakowie – wystawa miała miejsce w budynku U2 krakowskiej Akademii Górniczo Hutniczej. Poniżej zdjęcie tej wystawy zrobione w trakcie obrad Zjazdu.

Poniższa galeria wielościanów jednorodnych wklęsłych powstała na bazie konstrukcji każdego z nich przy użyciu cyrkla i linijki (również przestrzennych) w programie SketchUp a następnie utworzenia z nich gifów animowanych
WIELOŚCIANY JEDNORODNE WKLĘSŁE (Nonconvex uniform polyhedra)
Wielościany jednorodne wklęsłe symetrii czworościennej
Tu znajduje sie tylko jeden wielościan
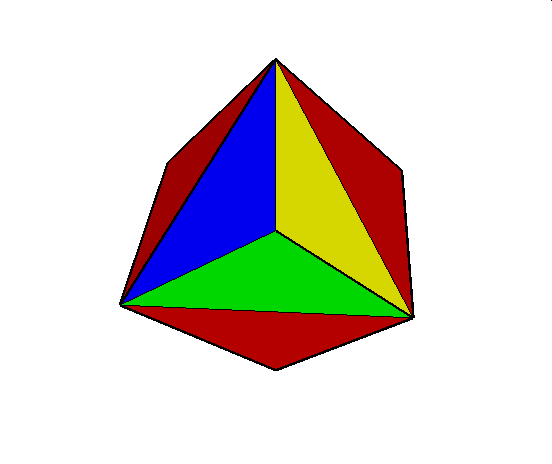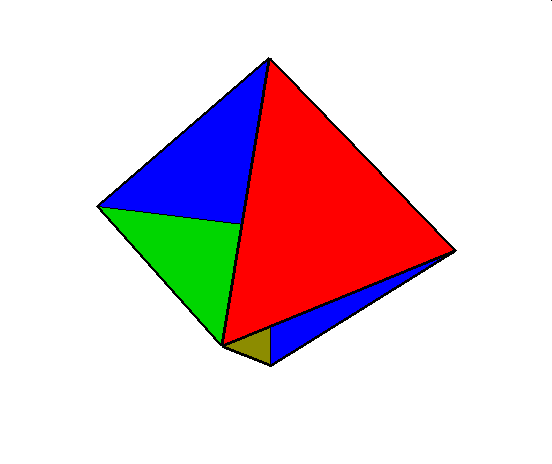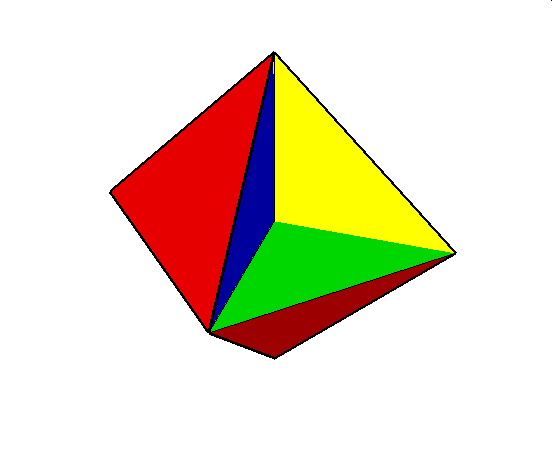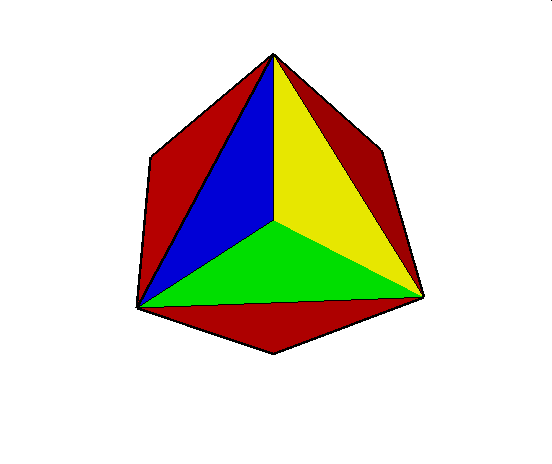 01. Tetrahemihexahedron (czworościennie wklęsły sześciościan)
01. Tetrahemihexahedron (czworościennie wklęsły sześciościan)
Wielościany jednorodne wklęsłe symetrii sześcienno-ośmiościennej)
Tych wielościanów jest dokładnie 10. Powstają z wielościanów archimedesowych symetrii sześciennej. Oto one:
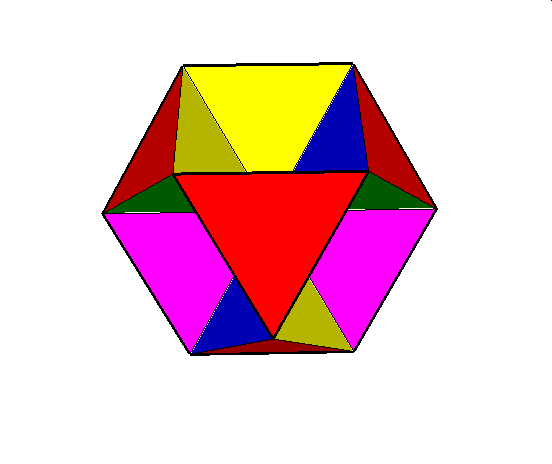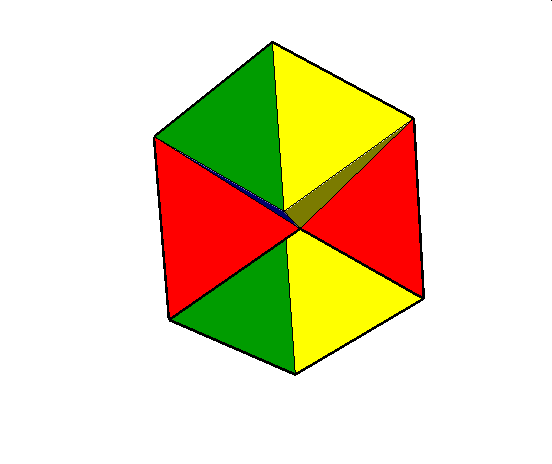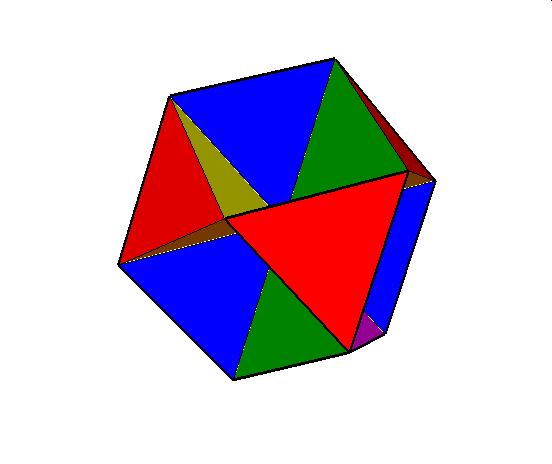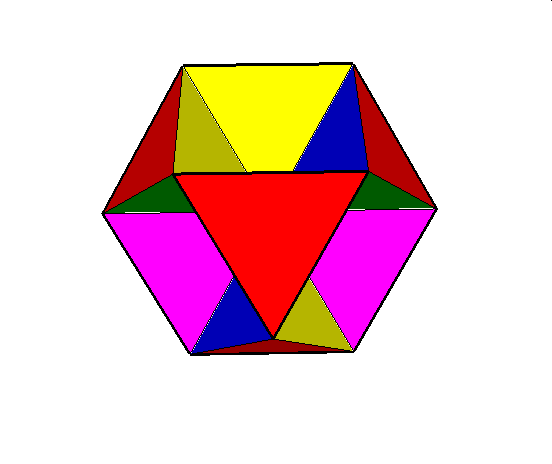 02. Octahemioctahedron (ośmiościennie wklęsły ośmiościan)
02. Octahemioctahedron (ośmiościennie wklęsły ośmiościan)
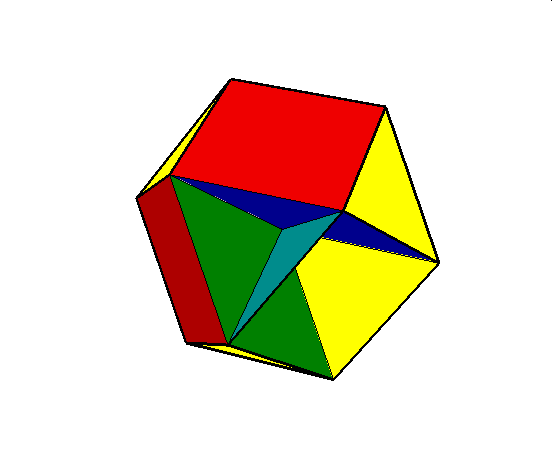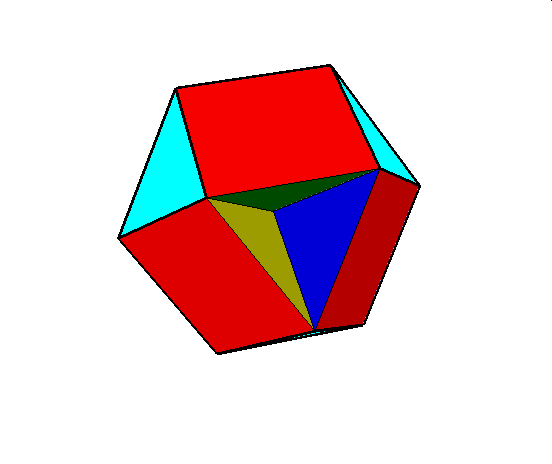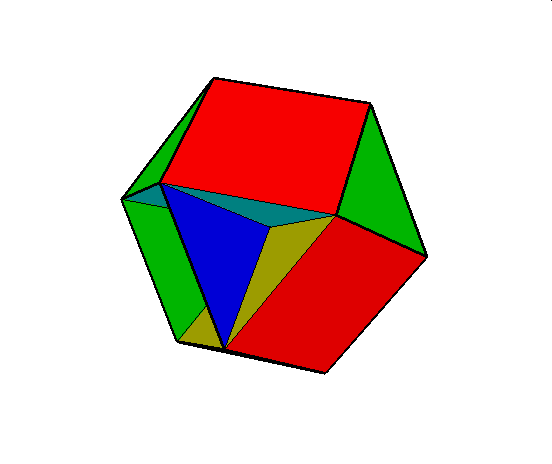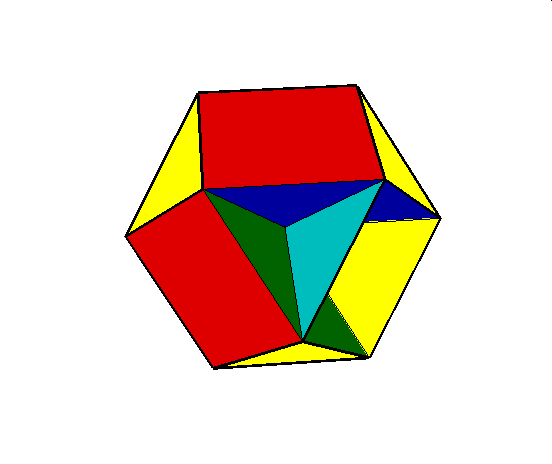 03. Cubohemioctahedron (sześciennie wklęsły ośmiościan)
03. Cubohemioctahedron (sześciennie wklęsły ośmiościan)
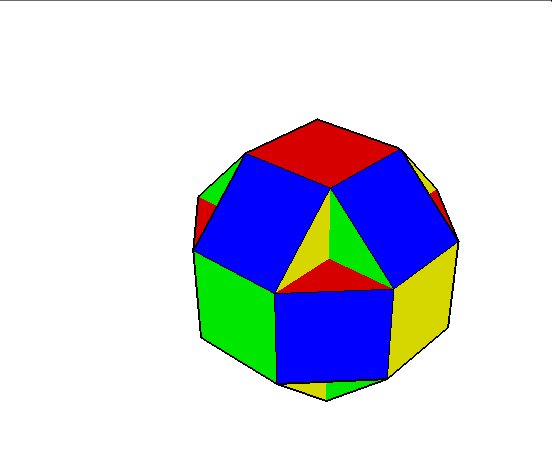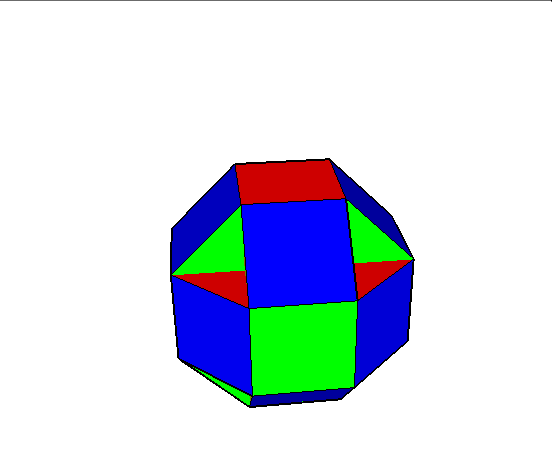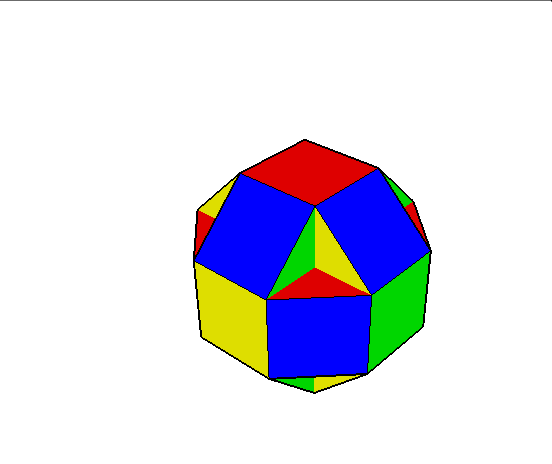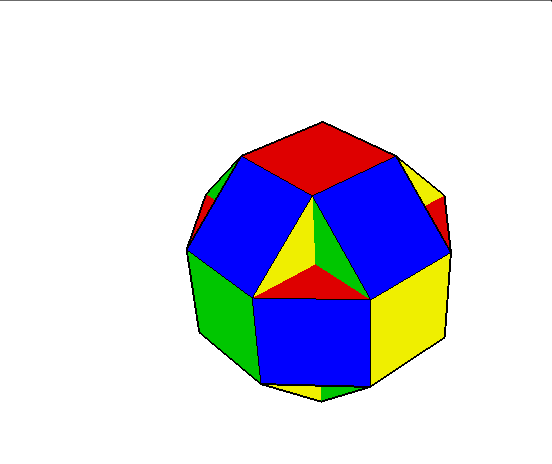
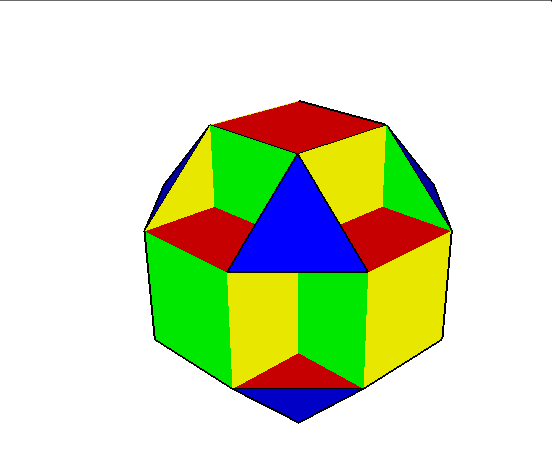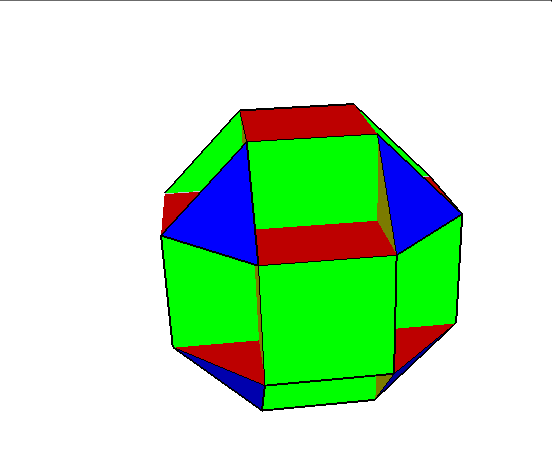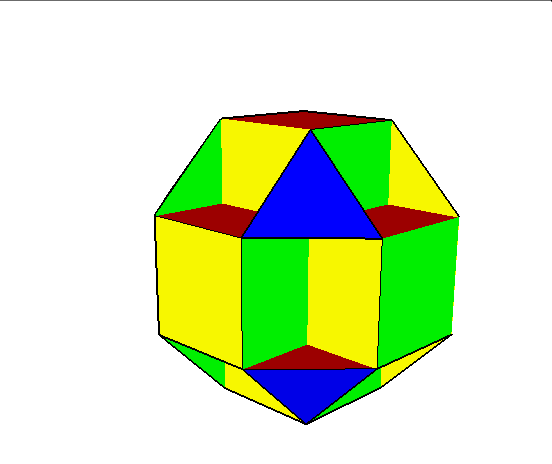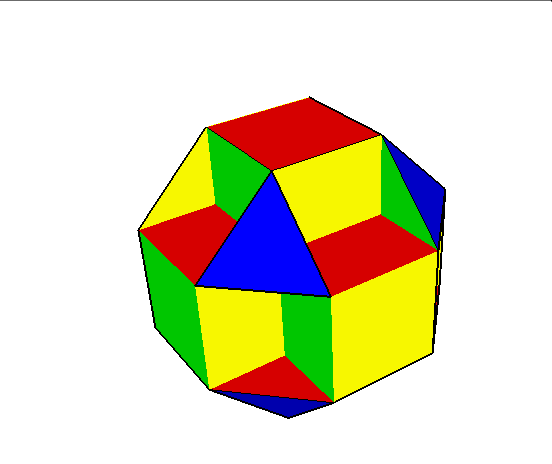 04. Cubocuboctahedron (sześcio sześcio ośmiościan)
04. Cubocuboctahedron (sześcio sześcio ośmiościan)
 05. Smallrhombihexahedron (mały rombowy sześciościan)
05. Smallrhombihexahedron (mały rombowy sześciościan)
 06. stellatedtruncatedhexahedron (ściety sześciościan gwiaździsty)
06. stellatedtruncatedhexahedron (ściety sześciościan gwiaździsty)
 07. Greatrhombihexahedron (wielki sześciościan rombowy)
07. Greatrhombihexahedron (wielki sześciościan rombowy)
 08. Greatcubicuboctahedron (wielki sześcio sześciościan)
08. Greatcubicuboctahedron (wielki sześcio sześciościan)
 09. Greatrhombicuboctahedron (wielki rombowy sześcioośmiościan)
09. Greatrhombicuboctahedron (wielki rombowy sześcioośmiościan)
 10. Cuboctatruncatedcuboctahedron (sześcioośmiościennie ścięty sześcioośmiościan)
10. Cuboctatruncatedcuboctahedron (sześcioośmiościennie ścięty sześcioośmiościan)
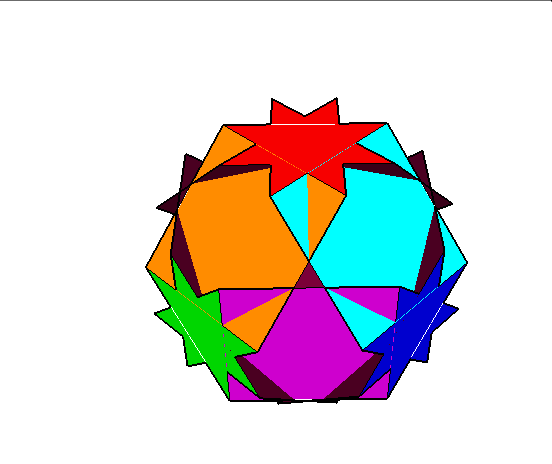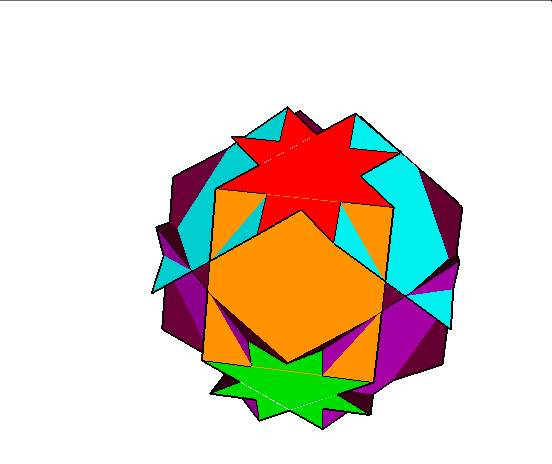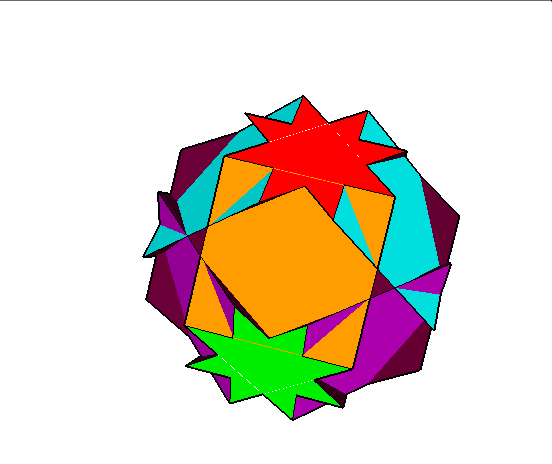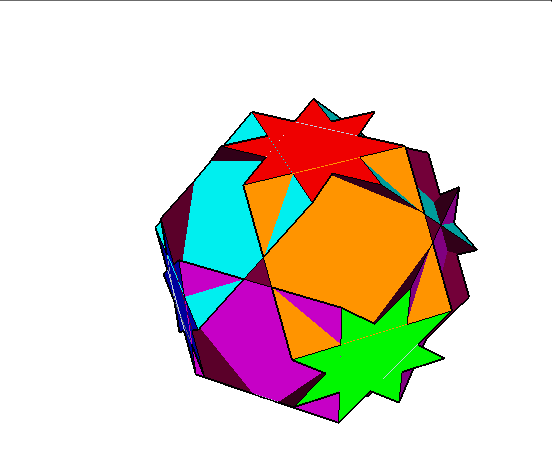 11. Greattruncatedcuboctahedron (wielki ścięty sześcioośmiościan)
11. Greattruncatedcuboctahedron (wielki ścięty sześcioośmiościan)
Wielościany jednorodne wklęsłe symetrii dwunasto-dwudziestościennej
Klasa tych wielościanów liczy łącznie 43 wielościany. Oto one:
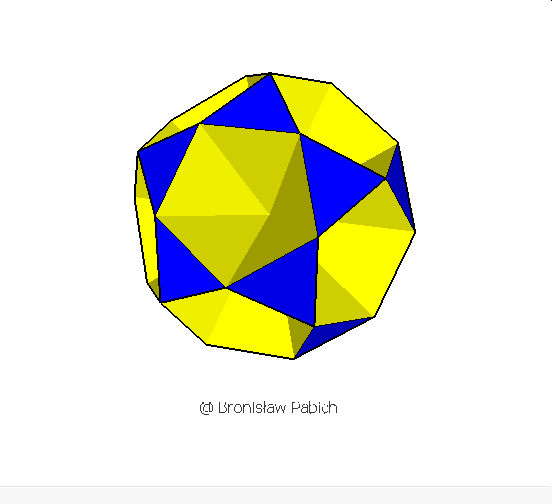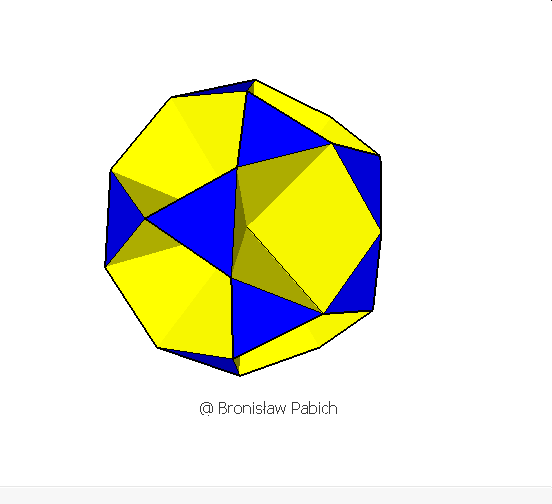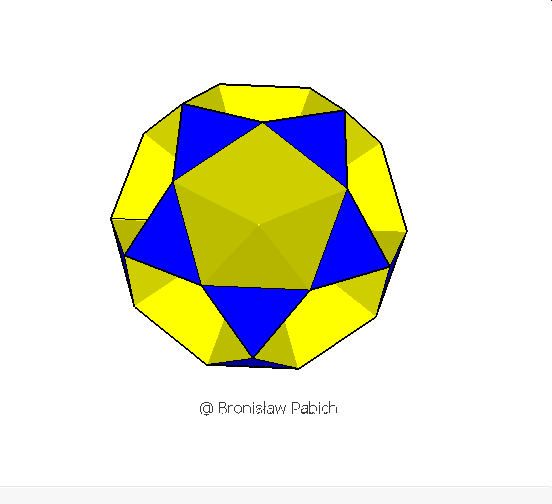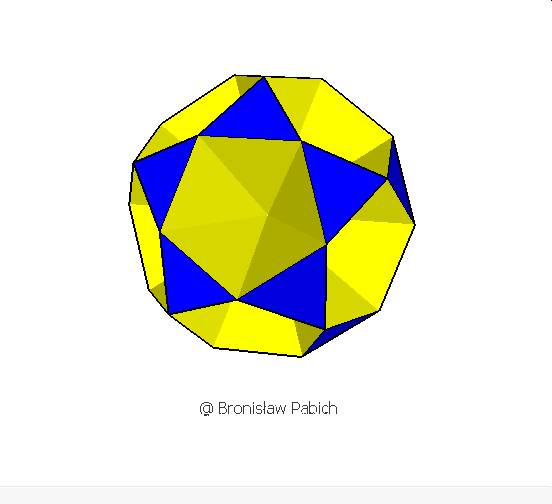 12. Smallicosihemidodecahedron (mały dwudziestościennie wklęsły dwunastościan)
12. Smallicosihemidodecahedron (mały dwudziestościennie wklęsły dwunastościan)
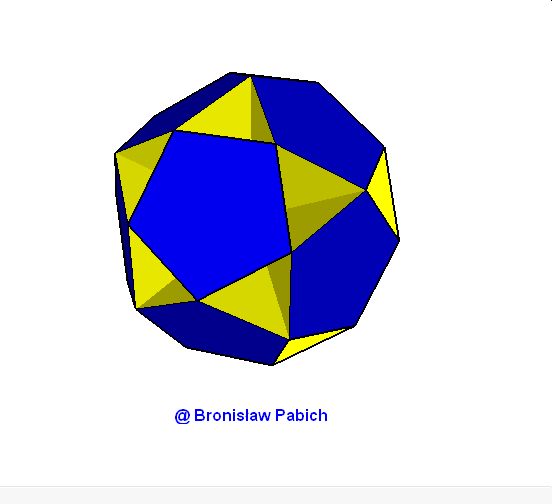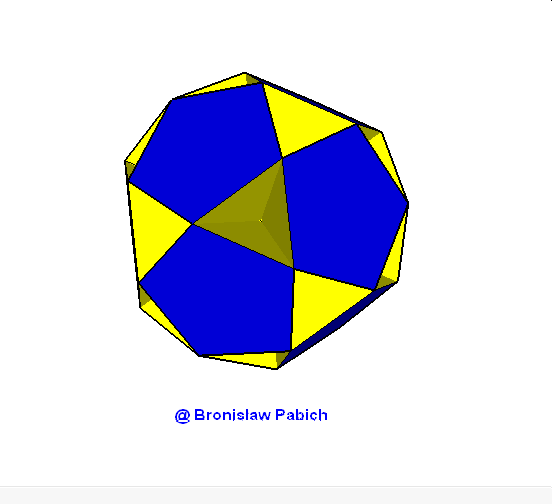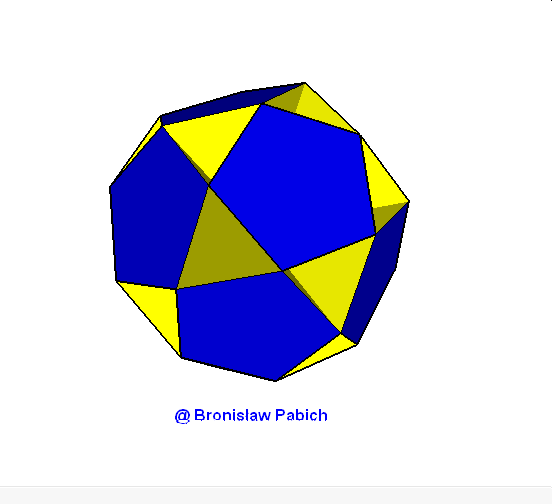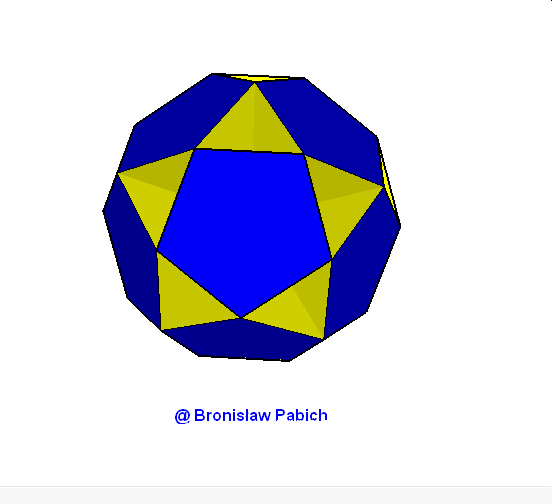 13. Smalldodecahemidodedacahedron (mały dwunastościennie wklęsły dwunastościan)
13. Smalldodecahemidodedacahedron (mały dwunastościennie wklęsły dwunastościan)
Zwróćmy uwagę na wieloscian 12 i 13. Różnia sie one tym, że zakryte wielokąty jednego z nich są otwarte w drugim i odwrotnie. Takie wielościany nazwałem bliźniaczymi. Które z wielościanów symetrii sześcienno-ośmiościennej są też bliźniacze?
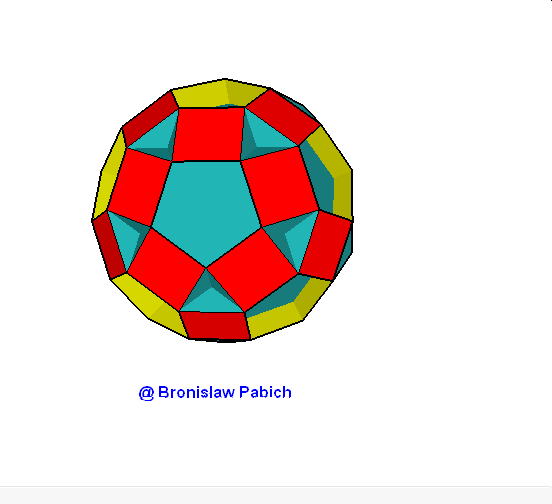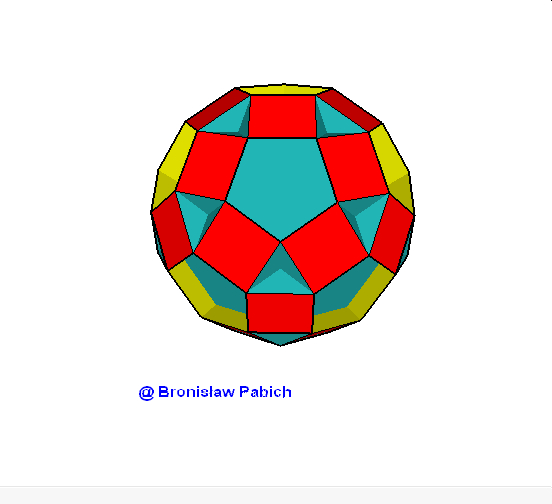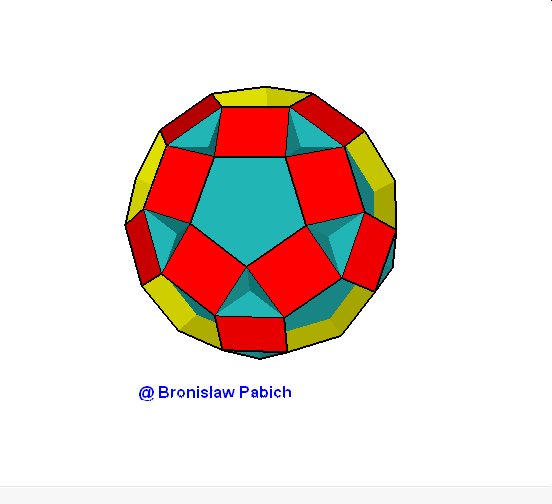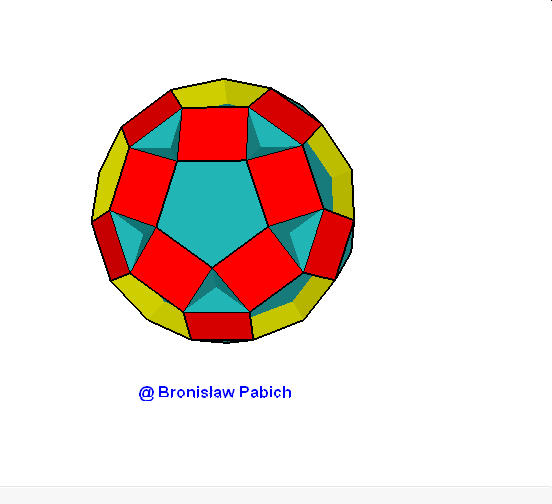 14. Smalldodecicosidodecahedron (mały dwunastodwudziesto dwunastościan).
14. Smalldodecicosidodecahedron (mały dwunastodwudziesto dwunastościan).
Zwróćmy uwagę, z którego wielościanu Archimedesa powstał wielościan 14?
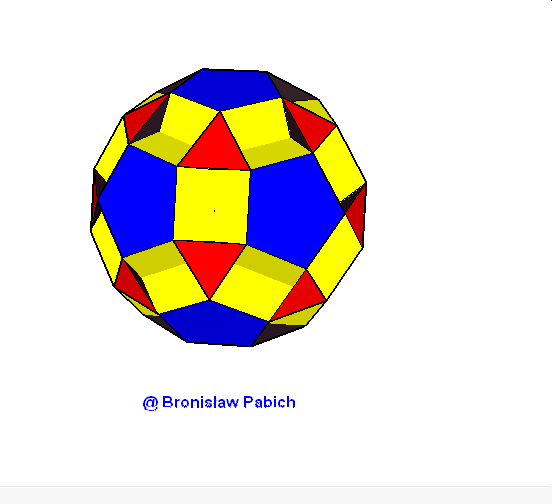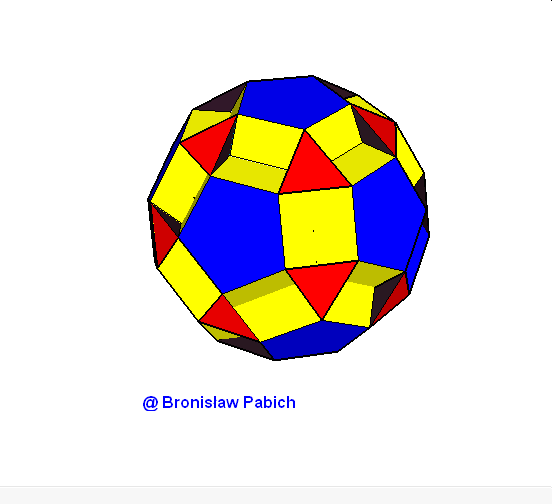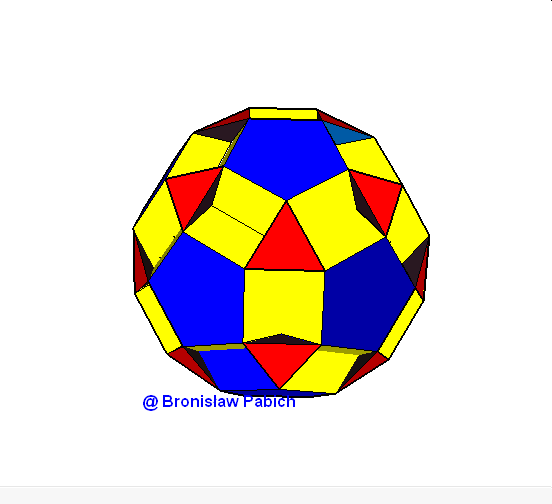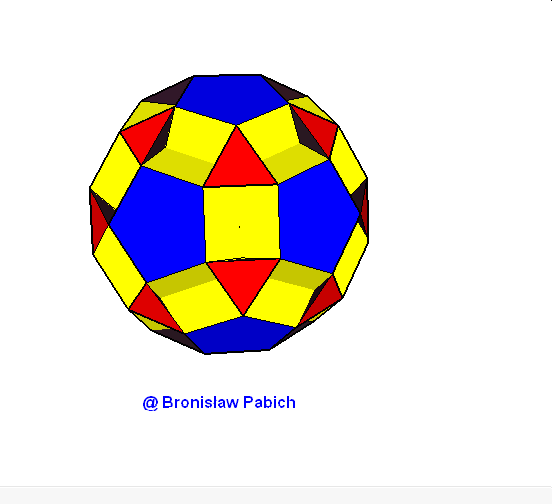 15. Smallrhombidodecahedron (mały dwunastościan rombowy)
15. Smallrhombidodecahedron (mały dwunastościan rombowy)
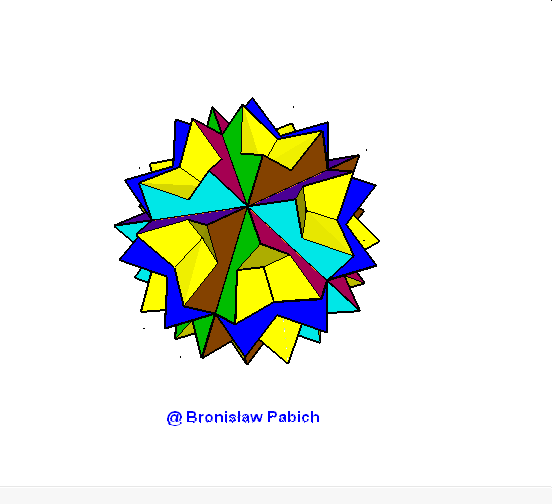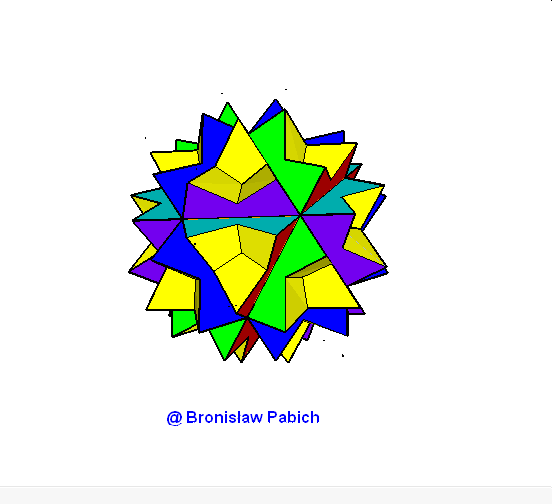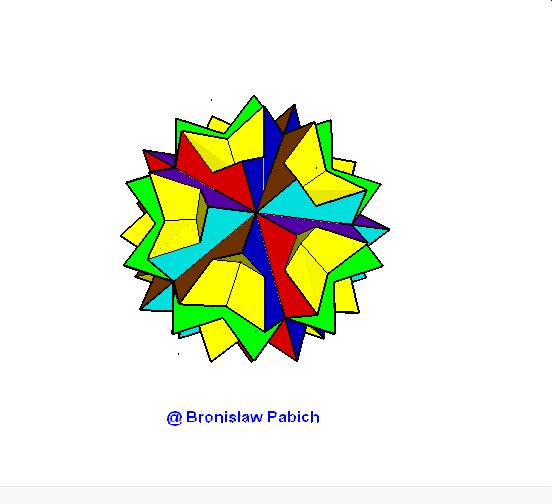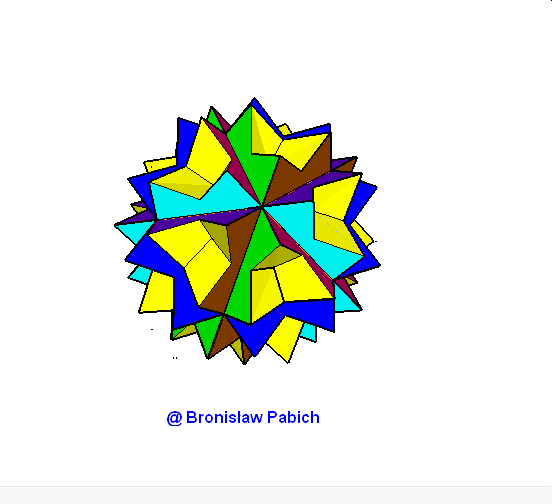 16. Greatstellatedtruncateddodecahedron (wielki ścięty gwiaździsty dwunastościan)
16. Greatstellatedtruncateddodecahedron (wielki ścięty gwiaździsty dwunastościan)
 17. Smallstellatedtruncateddodecahedron (mały ściety gwiaździsty dwunastościan)
17. Smallstellatedtruncateddodecahedron (mały ściety gwiaździsty dwunastościan)
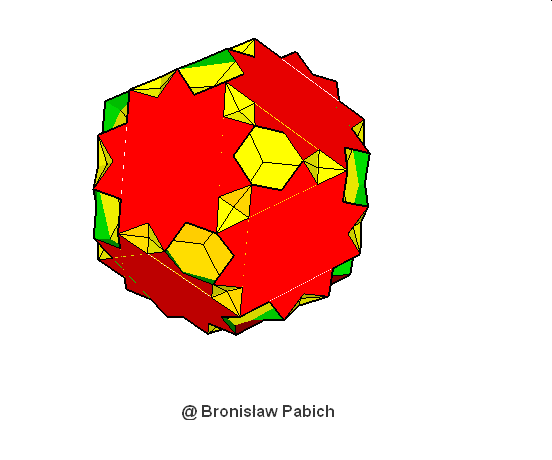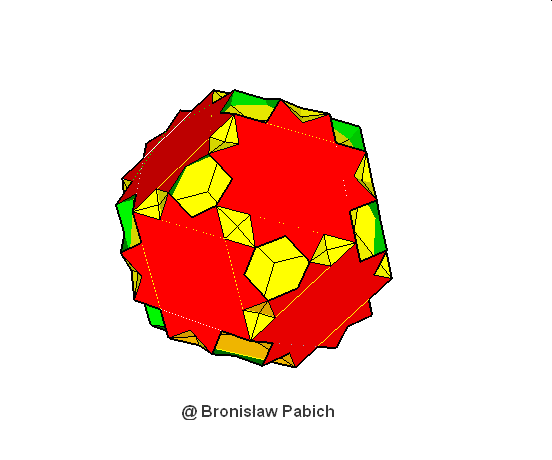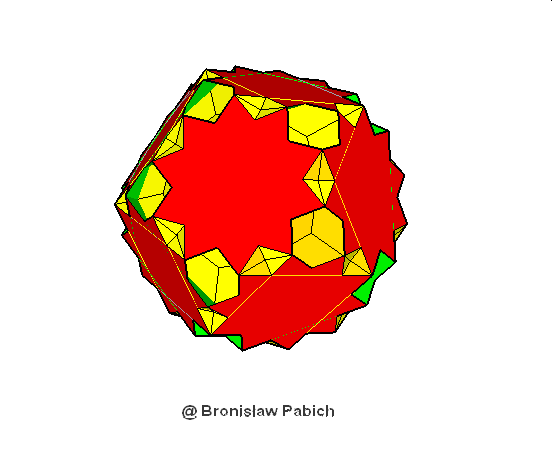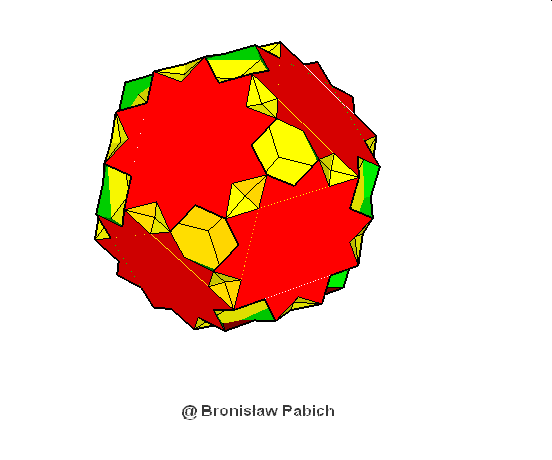 18. Greatdodecicoshedron (wielki dwunasto dwudziestościan)
18. Greatdodecicoshedron (wielki dwunasto dwudziestościan)
 19. Greatditrigonaldodecicosadodecahedron (wielki trójścienny dwunasto
19. Greatditrigonaldodecicosadodecahedron (wielki trójścienny dwunasto
dwudziestodwunastościan)
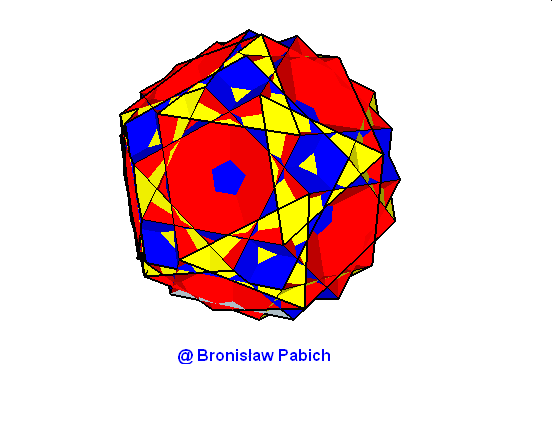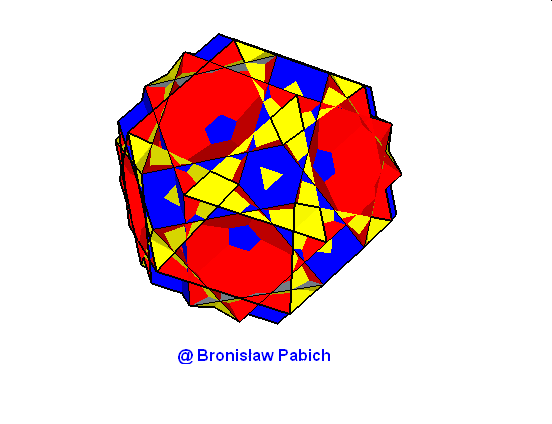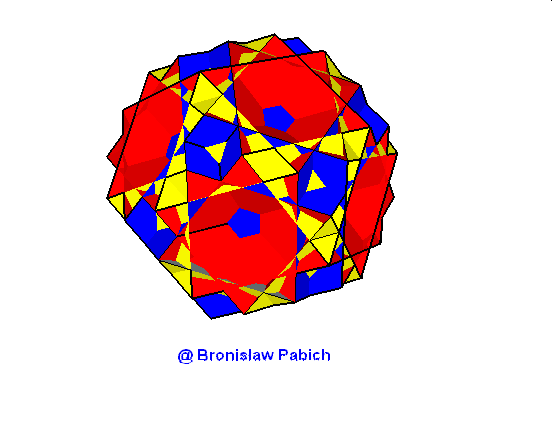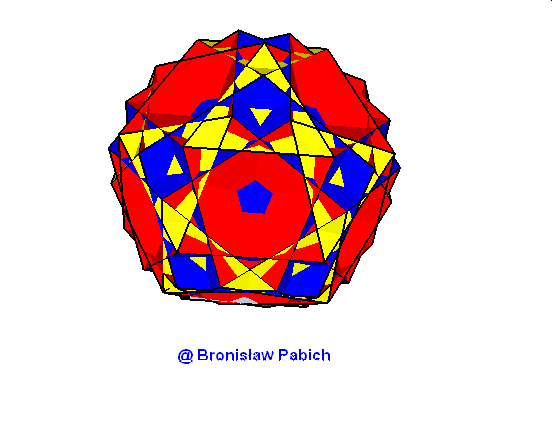 20. Greaticosicosidodecahedron (wielki dwudziestościenny dwudziestodwunastościan)
20. Greaticosicosidodecahedron (wielki dwudziestościenny dwudziestodwunastościan)
 21. Icositruncateddodecadodecahedron (dwudziestościennie ścięty dwunastodwunastościan)
21. Icositruncateddodecadodecahedron (dwudziestościennie ścięty dwunastodwunastościan)
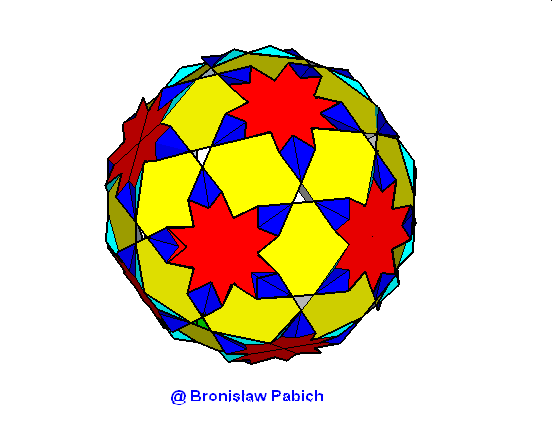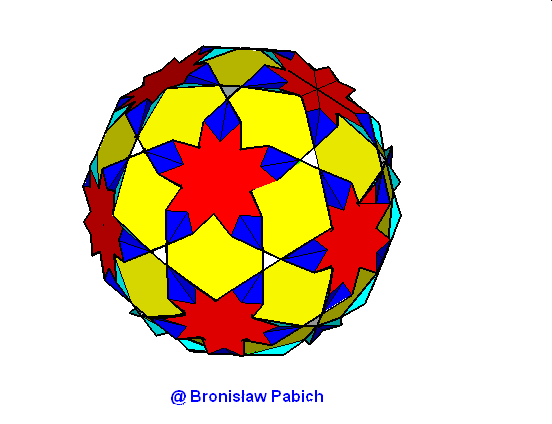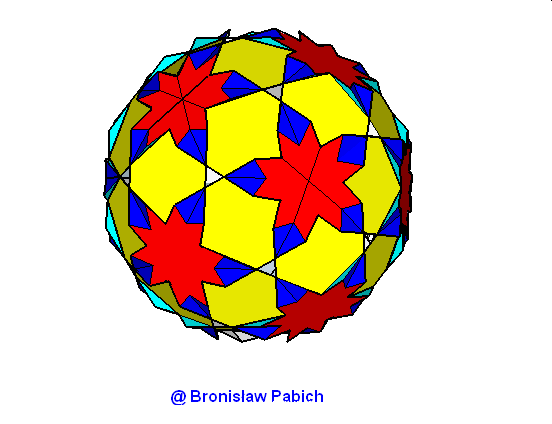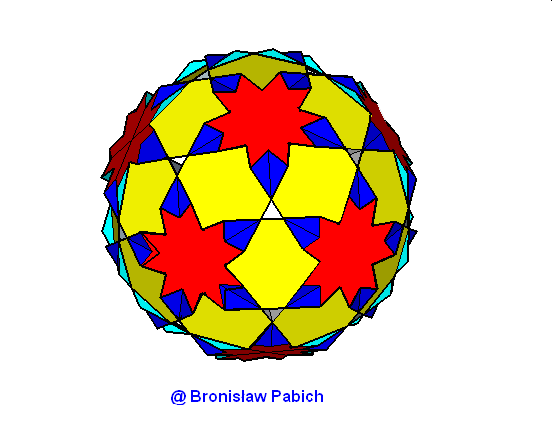 22. Truncateddodecadodecahedron (ścięty dwunasto dwunastościan)
22. Truncateddodecadodecahedron (ścięty dwunasto dwunastościan)
23. Greattruncatedicosidodacahedron (wielki ścięty dwunastościan) – chwilowo brak
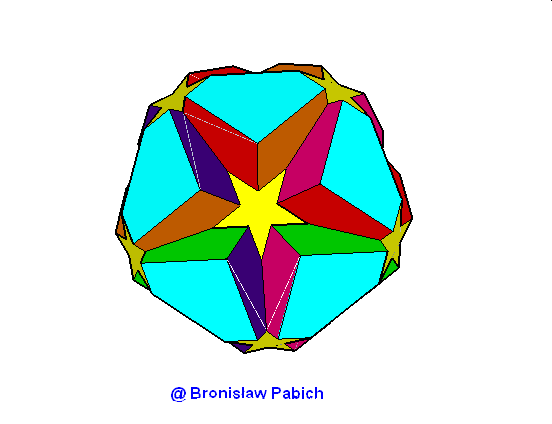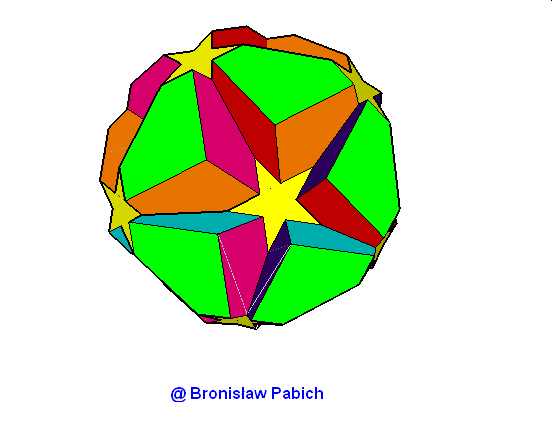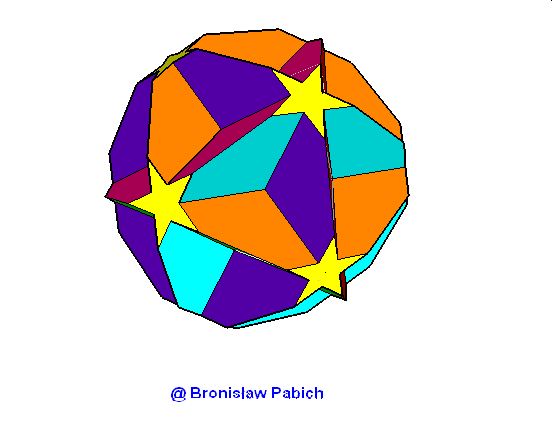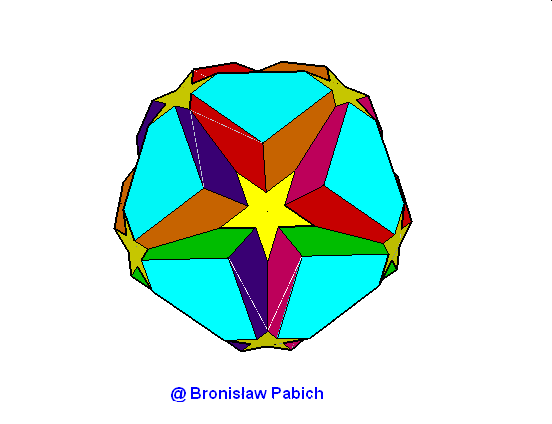 24. Greattruncateddodecahedron (wielki ściety dwunastościan)
24. Greattruncateddodecahedron (wielki ściety dwunastościan)
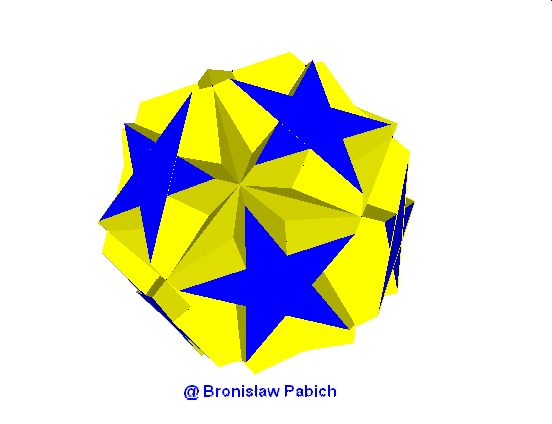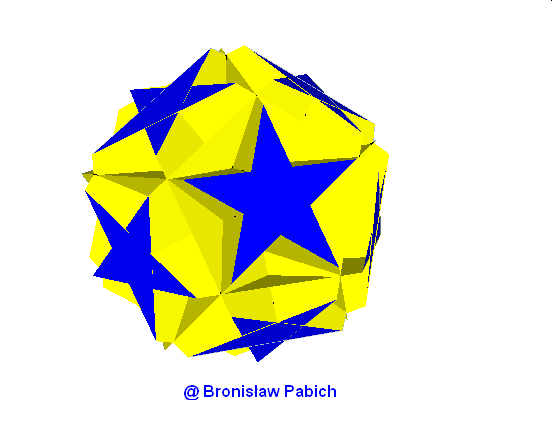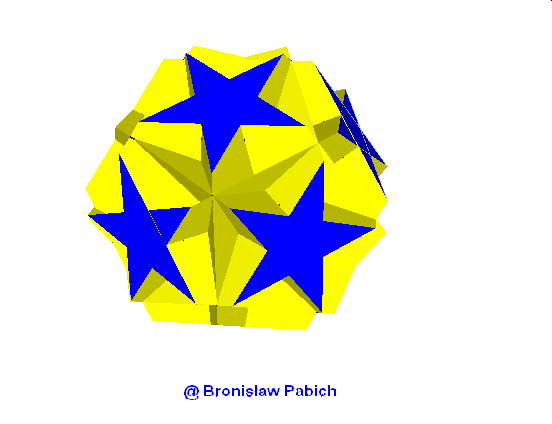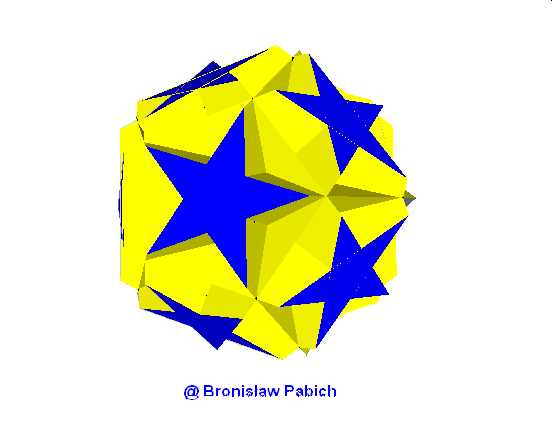 25. Greattruncatedicoshedron (wielki ścietydwudziestościan)
25. Greattruncatedicoshedron (wielki ścietydwudziestościan)
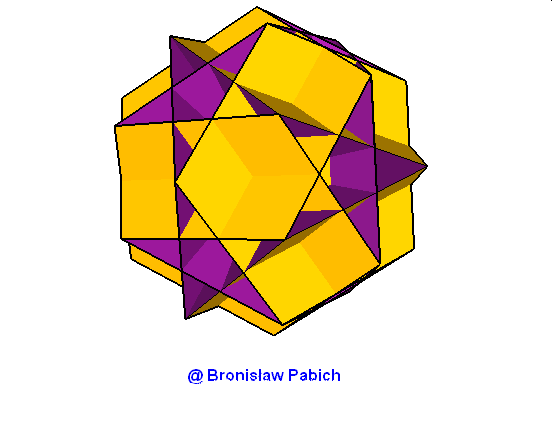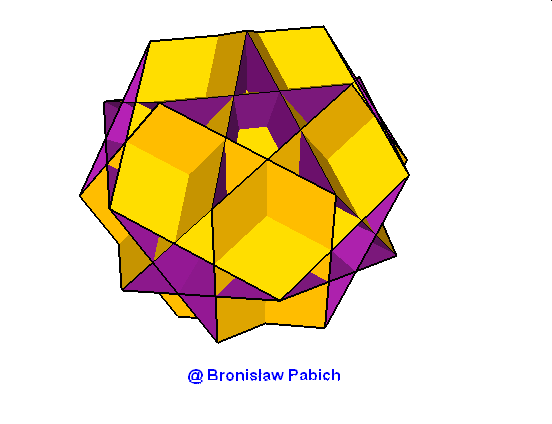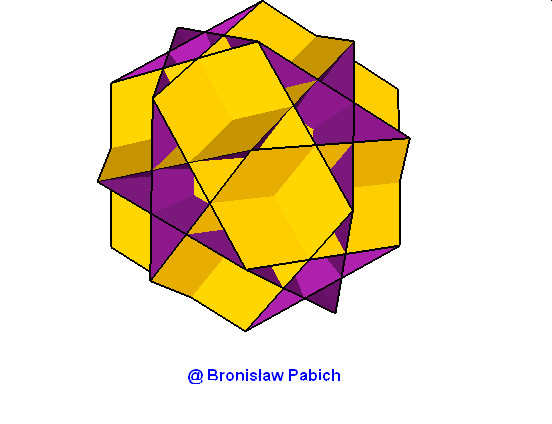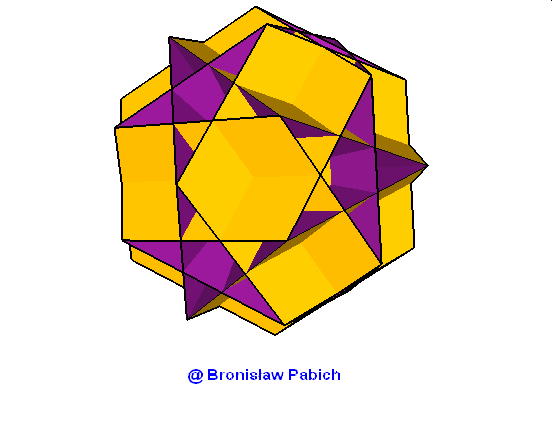 26. Greatdodecahemiicosahedron (wielki dwunastowklęsły dwudziestościan)
26. Greatdodecahemiicosahedron (wielki dwunastowklęsły dwudziestościan)
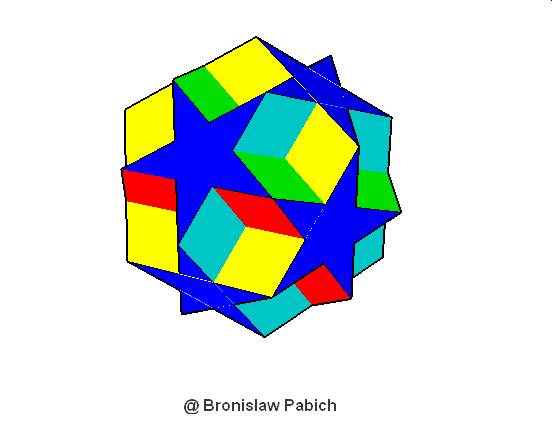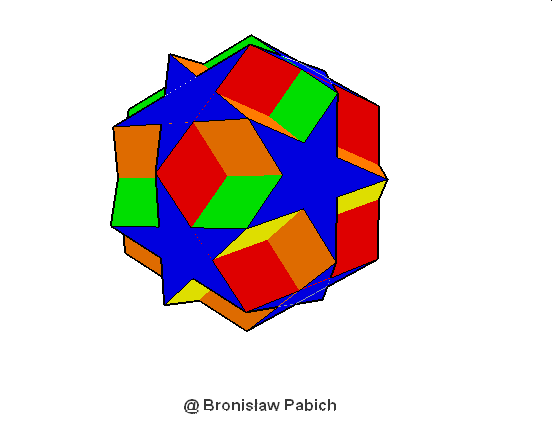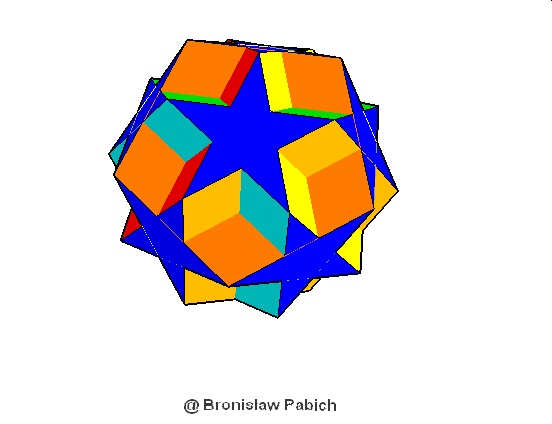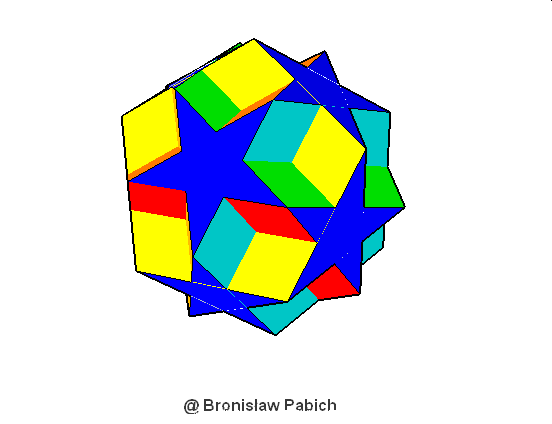 27. Dodecadodecahedron (dwunastodwunastościan)
27. Dodecadodecahedron (dwunastodwunastościan)
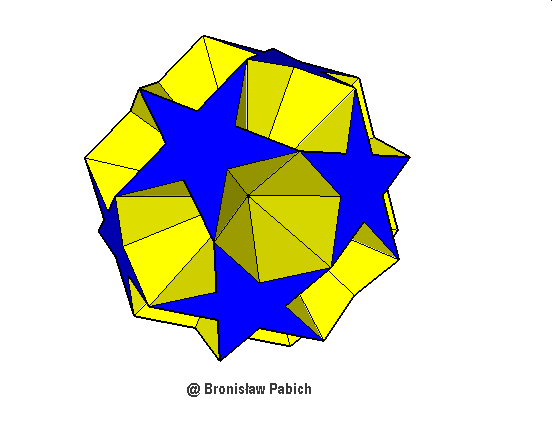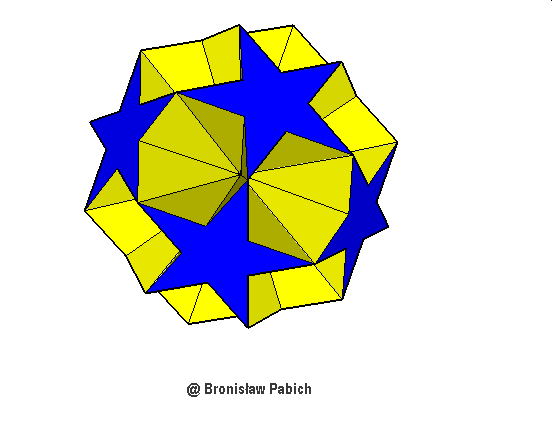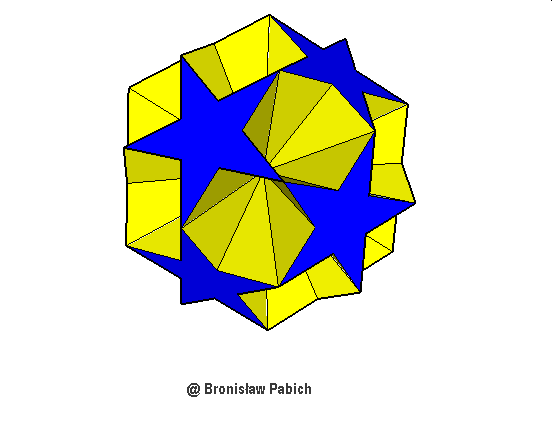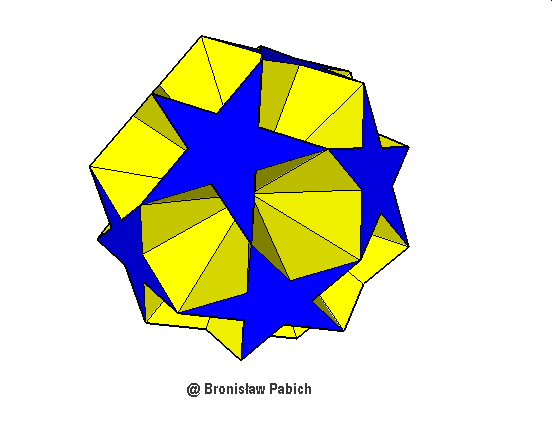 28. Smaldodecahemiicosahedron (mały dwunastowklęsły dwudziestościan)
28. Smaldodecahemiicosahedron (mały dwunastowklęsły dwudziestościan)
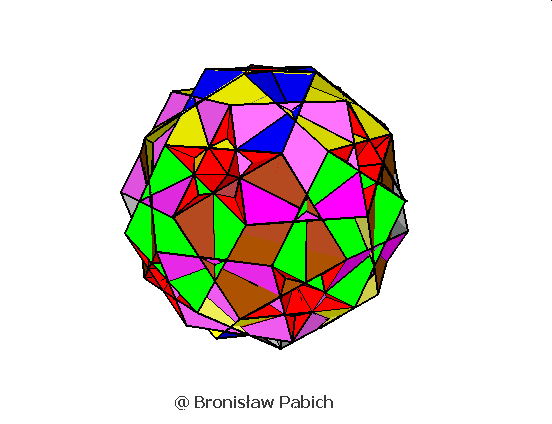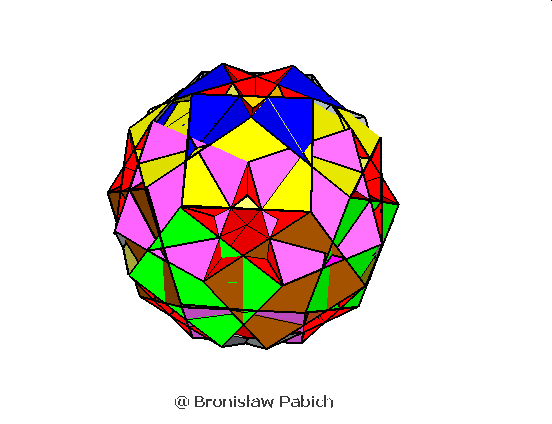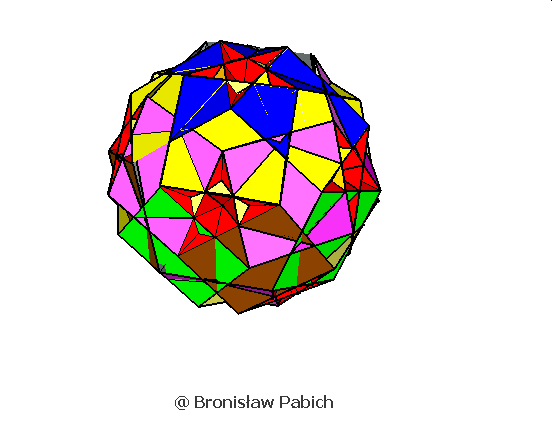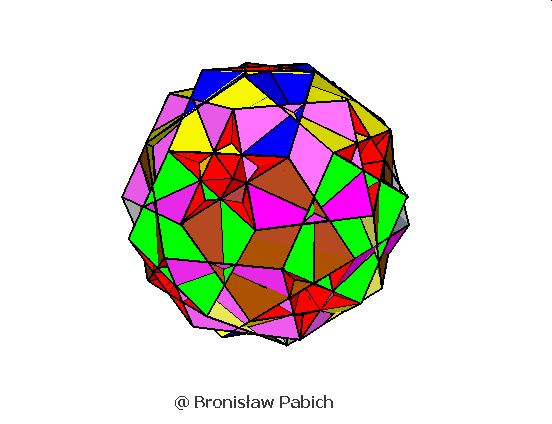 29. Rhombicosihedron (dwudziestościan rombowy)
29. Rhombicosihedron (dwudziestościan rombowy)
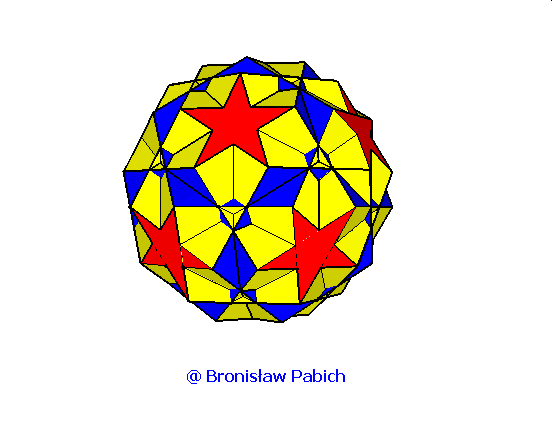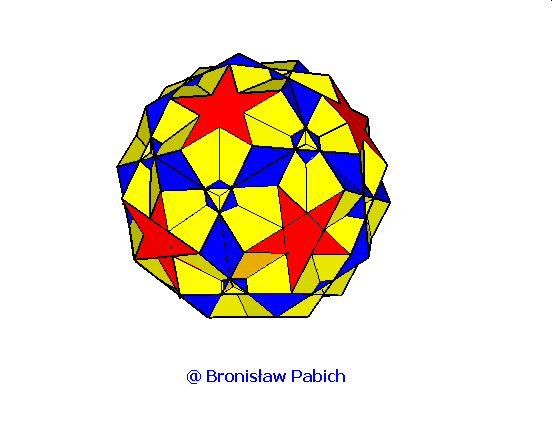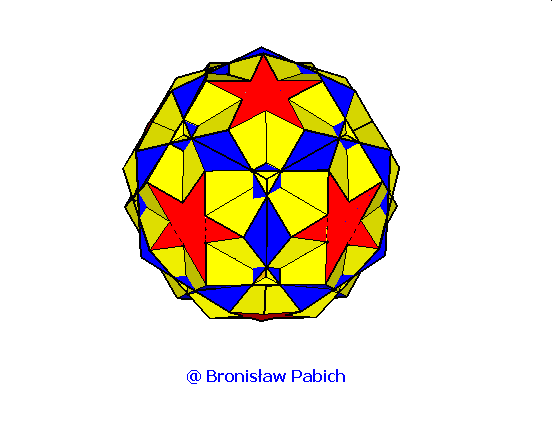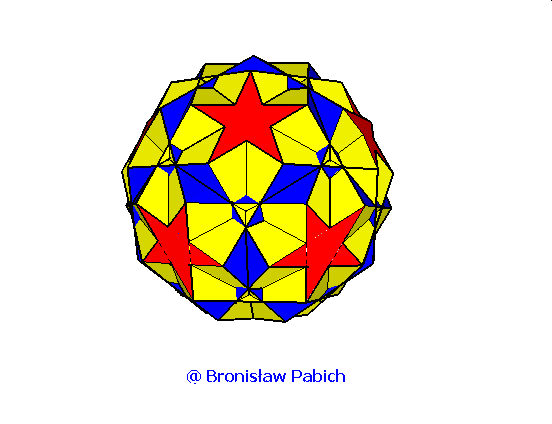 30. Rhombidodecadodecahedron (dwunastodwunastościan rombowy)
30. Rhombidodecadodecahedron (dwunastodwunastościan rombowy)
 31. Icosidodecdodecahedron (dwudziesto dwunasto dwunastościan)
31. Icosidodecdodecahedron (dwudziesto dwunasto dwunastościan)
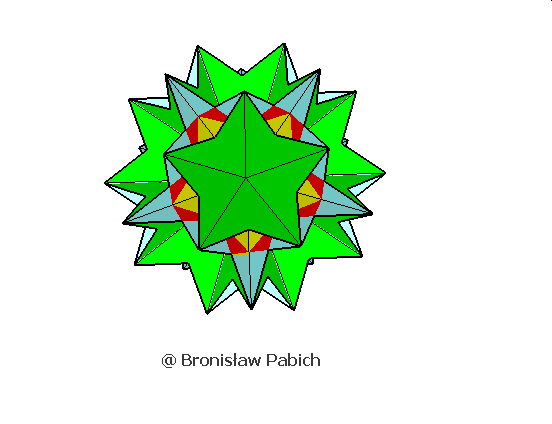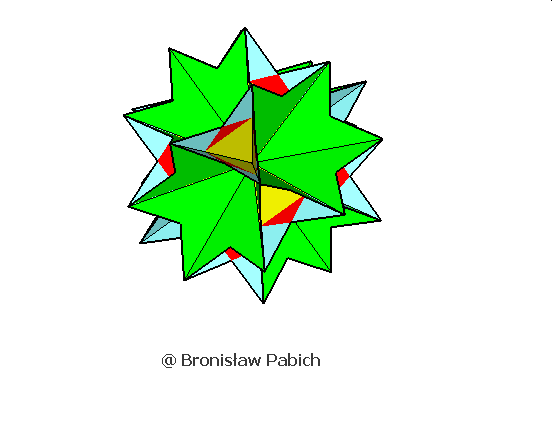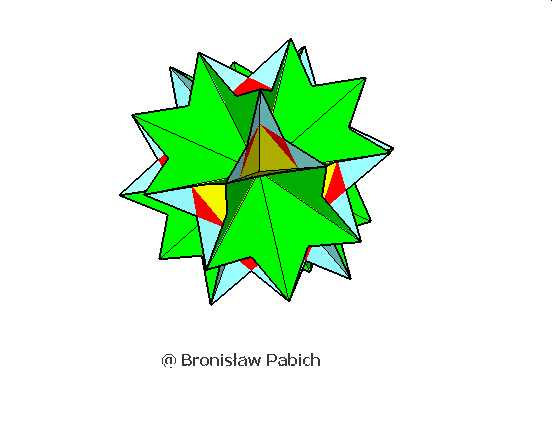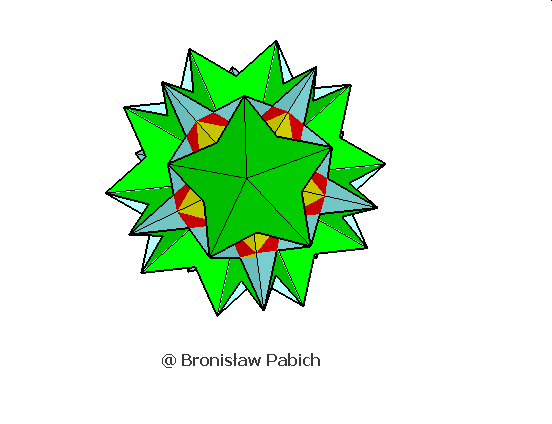 32. Greaticosihemidodecahedron (wielki dwudziestościęty dwunastościan)
32. Greaticosihemidodecahedron (wielki dwudziestościęty dwunastościan)
 33. Greaticosidodecahedron (wielki dwudziesto dwunastościan)
33. Greaticosidodecahedron (wielki dwudziesto dwunastościan)
 34. Greatdodecahemidodechedron (wielki dwunastościęty dwunastościan)
34. Greatdodecahemidodechedron (wielki dwunastościęty dwunastościan)
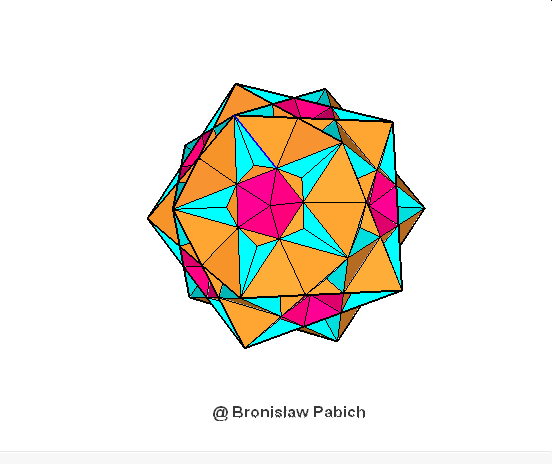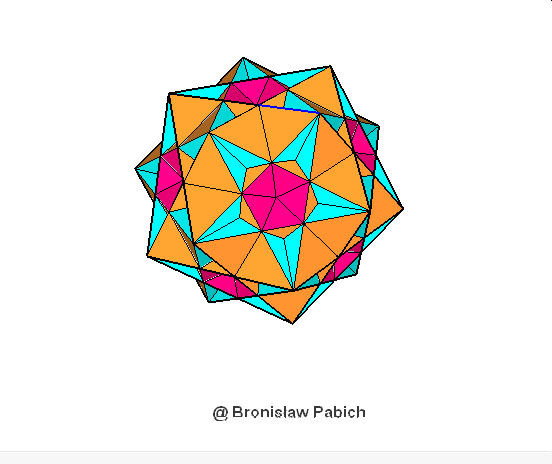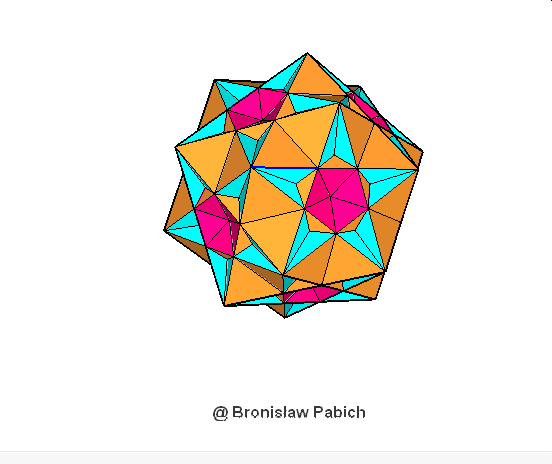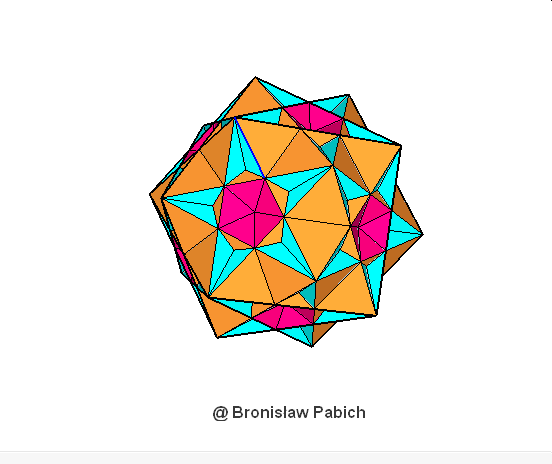 35. Greatditriginalicosidodecahedron (wielki trójścienny dwudziesto dwunastościan)
35. Greatditriginalicosidodecahedron (wielki trójścienny dwudziesto dwunastościan)
 36.Smallditrigonalicosidodecahedron (mały trójscienny dwudziesto dwunastościan)
36.Smallditrigonalicosidodecahedron (mały trójscienny dwudziesto dwunastościan)
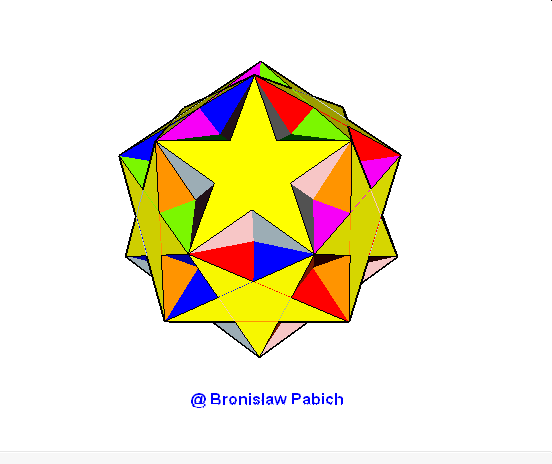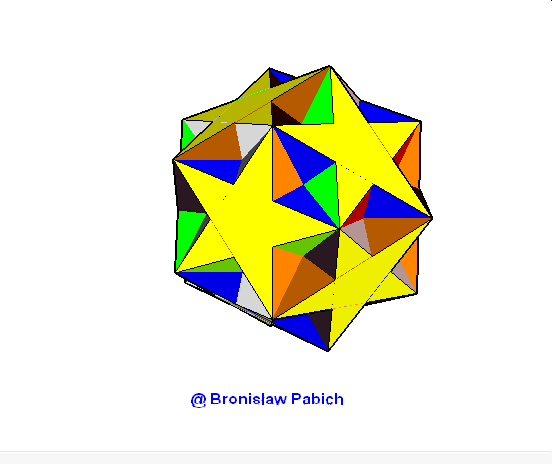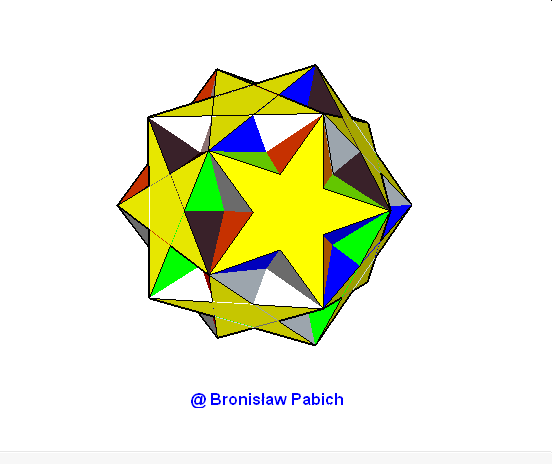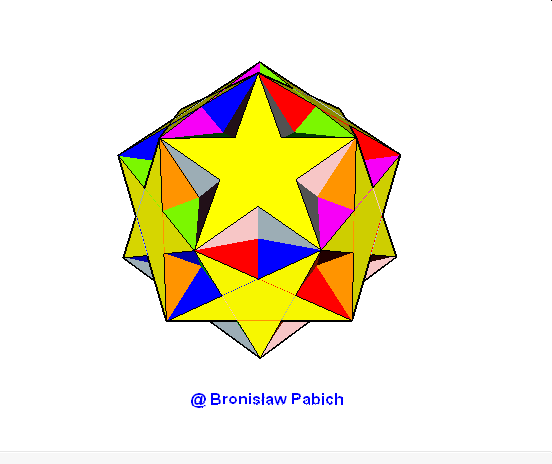 37. Ditrigonaldodecadodecahedron (trójścienny dwunastodwunastościan)
37. Ditrigonaldodecadodecahedron (trójścienny dwunastodwunastościan)
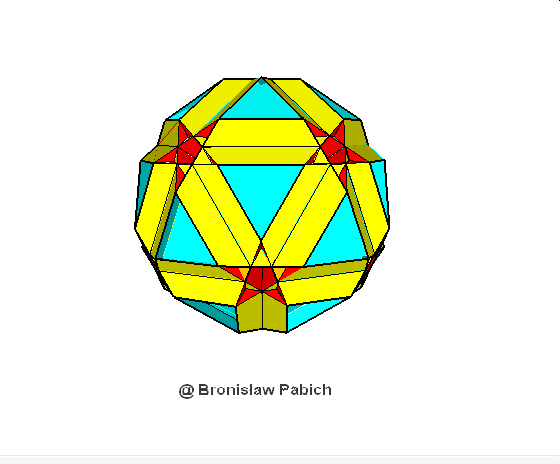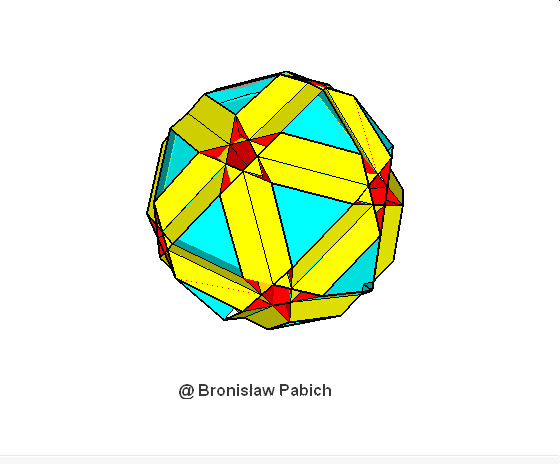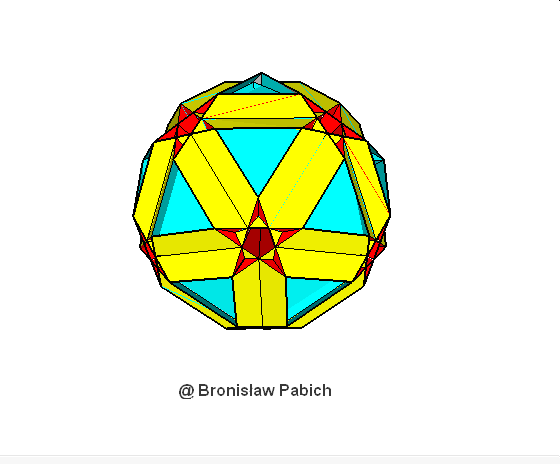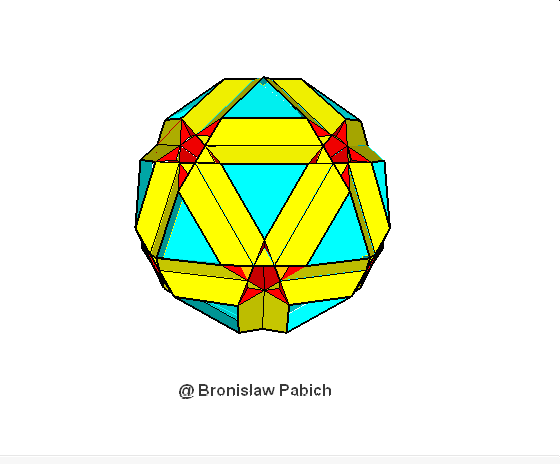 38. Smalldodecicosahedron (mały dwunastodwunastościan)
38. Smalldodecicosahedron (mały dwunastodwunastościan)
39. Smallicosiicosidodecahedron (mały dwudziesto dwudziesto dwunastościan)
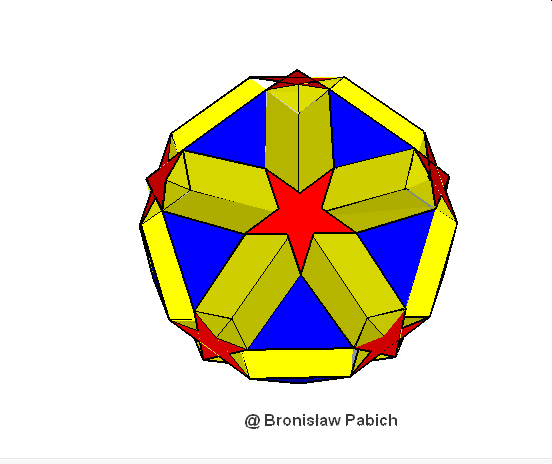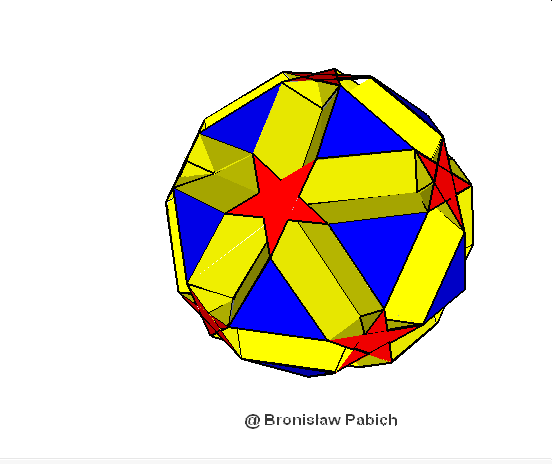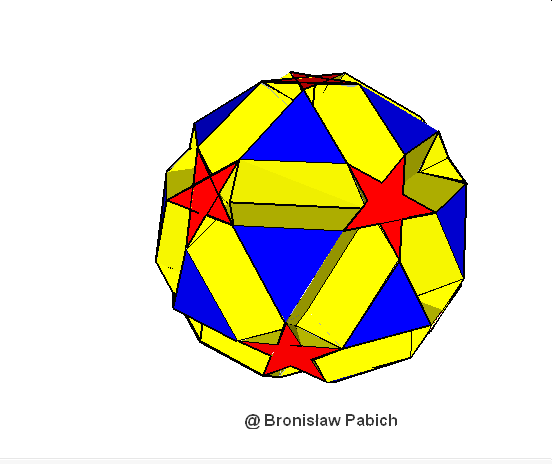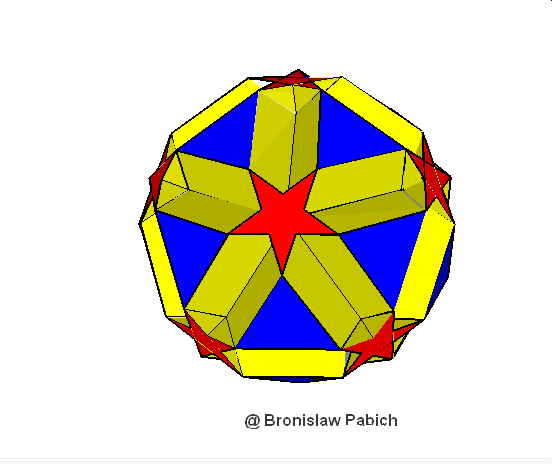 40. Smallditrigonaldodecisosidodecahedron (mały trójścienny dwunasto dwudziesto dwunastościan
40. Smallditrigonaldodecisosidodecahedron (mały trójścienny dwunasto dwudziesto dwunastościan
 41. Greatrhombidodecahedron (wielki dwunastościan rombowy)
41. Greatrhombidodecahedron (wielki dwunastościan rombowy)
 42. Greatdodecicosidodecahedron (wielki dwunastodwudziestodwunastościan)
42. Greatdodecicosidodecahedron (wielki dwunastodwudziestodwunastościan)